Inhalt Index DeskTop Bronstein
![]()
![]() Vektoranalysis und Feldtheorie Grundbegriffe der Feldtheorie Vektorfelder Koordinatendarstellung von Vektorfeldern
Vektoranalysis und Feldtheorie Grundbegriffe der Feldtheorie Vektorfelder Koordinatendarstellung von Vektorfeldern
Das Vektorfeld (13.12a) kann mit Hilfe dreier skalarer Felder ![]() und
und ![]() definiert werden, die als Koeffizienten des Vektors
definiert werden, die als Koeffizienten des Vektors ![]() bei seiner Zerlegung in drei beliebige inkomplanare Vektoren
bei seiner Zerlegung in drei beliebige inkomplanare Vektoren ![]() aufzufassen sind:
aufzufassen sind:
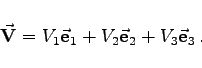 |
(13.16a) |
Wählt man für diese drei Vektoren die Einheitsvektoren der drei Koordinatenachsen ![]() , und drückt man die Koeffizienten V1, V2, V3 in kartesischen Koordinaten aus, dann gilt
, und drückt man die Koeffizienten V1, V2, V3 in kartesischen Koordinaten aus, dann gilt
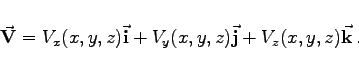 |
(13.16b) |
Somit kann das Vektorfeld mit Hilfe dreier skalarer Funktionen von drei skalaren Veränderlichen definiert werden.