Inhalt Index DeskTop Bronstein
![]()
![]() Vektoranalysis und Feldtheorie Räumliche Differentialoperationen Nablaoperator, Laplace-Operator
Vektoranalysis und Feldtheorie Räumliche Differentialoperationen Nablaoperator, Laplace-Operator
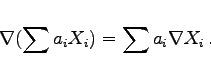 |
(13.66) |
 |
(13.67) |
addiert. Daraufhin werden die auf diese Weise erhaltenen Produkte nach den Regeln der Vektoralgebra derart umgeformt, daß nach dem Operator ![]() nur der mit dem Zeichen
nur der mit dem Zeichen ![]() gekennzeichnete Faktor steht. Nach Abschluß der Rechnung wird das Zeichen weggelassen.
gekennzeichnete Faktor steht. Nach Abschluß der Rechnung wird das Zeichen weggelassen.
| Beispiel A |
|
|
| Beispiel B |
|
|