Inhalt Index DeskTop Bronstein
![]()
![]() Vektoranalysis und Feldtheorie Räumliche Differentialoperationen Nablaoperator, Laplace-Operator
Vektoranalysis und Feldtheorie Räumliche Differentialoperationen Nablaoperator, Laplace-Operator
Nablaoperator wird ein symbolischer Vektor ![]() genannt, der häufig zur Darstellung von räumlichen Differentialoperationen benutzt wird und dessen Einführung Berechnungen in der Vektoranalysis vereinfacht. Für die Operatoren Gradient, Vektorgradient, Divergenz und Rotation gelten die folgenden Formeln:
genannt, der häufig zur Darstellung von räumlichen Differentialoperationen benutzt wird und dessen Einführung Berechnungen in der Vektoranalysis vereinfacht. Für die Operatoren Gradient, Vektorgradient, Divergenz und Rotation gelten die folgenden Formeln:
Gradient von![]()
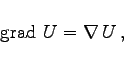 |
(13.65a) |
 |
(13.65b) |
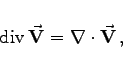 |
(13.65c) |
 |
(13.65d) |
In kartesischen Koordinaten gilt:
Die Komponenten des Nablaoperators sind als partielle Ableitungsoperatoren aufzufassen, d.h., das Symbol ![]() schreibt die partielle Ableitung nach x vor, wobei die anderen Variablen als Konstanten betrachtet werden. Die Formeln für die räumlichen Differentialoperatoren in kartesischen Koordinaten ergeben sich durch formale Multiplikation dieses Vektoroperators mit dem Skalar U oder dem Vektor
schreibt die partielle Ableitung nach x vor, wobei die anderen Variablen als Konstanten betrachtet werden. Die Formeln für die räumlichen Differentialoperatoren in kartesischen Koordinaten ergeben sich durch formale Multiplikation dieses Vektoroperators mit dem Skalar U oder dem Vektor ![]() .
.