Inhalt Index DeskTop Bronstein
![]()
![]() Funktionentheorie Funktionen einer komplexen Veränderlichen Konforme Abbildung Komplexe Potentiale
Funktionentheorie Funktionen einer komplexen Veränderlichen Konforme Abbildung Komplexe Potentiale
Es wird ein Feld ![]() in der x,y-Ebene mit den stetigen und differenzierbaren Komponenten vx(x,y) und vy(x,y) des Vektors
in der x,y-Ebene mit den stetigen und differenzierbaren Komponenten vx(x,y) und vy(x,y) des Vektors ![]() für den quellenfreien und den wirbelfreien Fall betrachtet.
für den quellenfreien und den wirbelfreien Fall betrachtet.
 .
.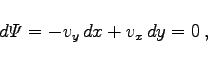 |
(14.20a) |
und es gilt:
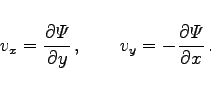 |
(14.20b) |
Für zwei Punkte ![]() des Feldes
des Feldes ![]() ist die Differenz
ist die Differenz ![]() ein Maß für den Vektorfluß durch eine Kurve, die die Punkte P1 und P2 verbindet, falls diese Kurve ganz im Feld verläuft.
ein Maß für den Vektorfluß durch eine Kurve, die die Punkte P1 und P2 verbindet, falls diese Kurve ganz im Feld verläuft.
 :
: |
(14.21a) |
und es gilt
 |
(14.21b) |
Die Funktionen ![]() und
und ![]() genügen den CAUCHY-RIEMANNschen Differentialgleichungen, und jede für sich erfüllt die LAPLACEsche Differentialgleichung (
genügen den CAUCHY-RIEMANNschen Differentialgleichungen, und jede für sich erfüllt die LAPLACEsche Differentialgleichung (![]() ). Man faßt
). Man faßt ![]() und
und ![]() zu der analytischen Funktion
zu der analytischen Funktion
 |
(14.22) |
zusammen und bezeichnet diese Funktion als komplexes Potential des Feldes ![]() . Danach ist
. Danach ist ![]() das Potential des Vektorfeldes
das Potential des Vektorfeldes ![]() im Sinne der in der Physik und Elektrotechnik üblichen Bezeichnungsweise. Die Linien
im Sinne der in der Physik und Elektrotechnik üblichen Bezeichnungsweise. Die Linien ![]() und
und ![]() bilden ein orthogonales Netz. Für die Ableitung des komplexen Potentials und den Feldvektor
bilden ein orthogonales Netz. Für die Ableitung des komplexen Potentials und den Feldvektor ![]() gelten die Beziehungen:
gelten die Beziehungen:
 |
(14.23) |