Inhalt Index DeskTop Bronstein
![]()
![]() Funktionentheorie Integration im Komplexen Bestimmtes und unbestimmtes Integral Eigenschaften und Berechnung komplexer Integrale
Funktionentheorie Integration im Komplexen Bestimmtes und unbestimmtes Integral Eigenschaften und Berechnung komplexer Integrale
Sind der Integrationsweg ![]() (oder die Kurve K) in der Form
(oder die Kurve K) in der Form
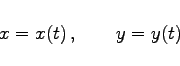 |
(14.37) |
und die t-Werte für den Anfangs- und den Endpunkt als tA und tB gegeben, dann kann das komplexe bestimmte Integral über zwei reelle Kurvenintegrale berechnet werden. Dazu wird der Integrand in Real- und Imaginärteil aufgespaltet, und man erhält:
 |
= |  |
|
| = | 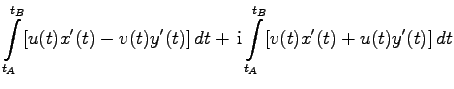 |
(14.38a) |
mit
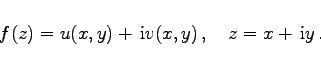 |
(14.38b) |
| Beispiel |
|
|