Inhalt Index DeskTop Bronstein
![]()
![]() Funktionentheorie Integration im Komplexen Bestimmtes und unbestimmtes Integral Eigenschaften und Berechnung komplexer Integrale
Funktionentheorie Integration im Komplexen Bestimmtes und unbestimmtes Integral Eigenschaften und Berechnung komplexer Integrale
Wenn die Integration einer Funktion f(z), die in einem einfach zusammenhängenden Gebiet analytisch ist, über einen geschlossenen Integrationsweg K erfolgt, der dieses Gebiet begrenzt, dann ist der Wert des Integrals gemäß dem Integralsatz von CAUCHY gleich Null:
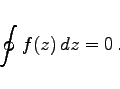 |
(14.39) |
Enthält dieses Gebiet singuläre Punkte, dann ist der Wert des Integrals mit Hilfe des Residuensatzes zu berechnen.
| Beispiel |
|
Für die Funktion |