Inhalt Index DeskTop Bronstein
![]()
![]() Wahrscheinlichkeitsrechnung und Mathematische Statistik Mathematische Statistik Monte-Carlo-Methode Zufallszahlen
Wahrscheinlichkeitsrechnung und Mathematische Statistik Mathematische Statistik Monte-Carlo-Methode Zufallszahlen
Man versteht unter gleichverteilten Zufallszahlen die im Intervall [0,1] gleichverteilten Zufallszahlen, die als Realisierung einer Zufallsgröße X mit der folgenden Dichtefunktion f0(x) und der folgenden Verteilungsfunktion F0(x) interpretiert werden:
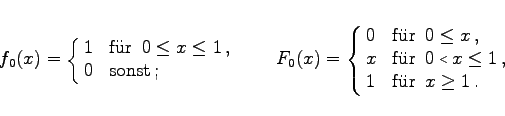 |
(16.171) |
Dieser Algorithmus hat sich bei praktischen Anwendungen nicht bewährt. Er liefert mehr kleine Werte, als in der Regel gebraucht werden. Deshalb wurden verschiedene andere Methoden entwickelt.
berechnet. Dabei ist z0 eine beliebige positive Zahl; c und m sind ebenfalls ganze positive Zahlen, die geeignet zu wählen sind. Für zi+1 ist die kleinste nicht negative ganze Zahl zu nehmen, die der Kongruenz (16.172) genügt. Die Zahlen zi/m liegen zwischen 0 und 1 und können als gleichverteilte Zufallszahlen dienen.