Inhalt Index DeskTop Bronstein
![]()
![]() Wahrscheinlichkeitsrechnung und Mathematische Statistik Mathematische Statistik Monte-Carlo-Methode Anwendungen der Monte-Carlo-Methode in der numerischen Mathematik
Wahrscheinlichkeitsrechnung und Mathematische Statistik Mathematische Statistik Monte-Carlo-Methode Anwendungen der Monte-Carlo-Methode in der numerischen Mathematik
Zunächst soll für Funktionen einer Variablen die Transformation des bestimmten Integrals
auf einen Ausdruck gezeigt werden, der das Integral
 |
(16.178) |
enthält. Danach kann die Monte-Carlo-Methode gemäß Beispiel für eine Monte-Carlo-Simulation angewendet werden. Man substituiert wie folgt:
Dadurch geht (16.177) über in
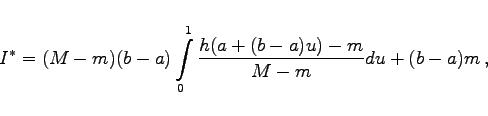 |
(16.180) |
wobei der Integrand  der Bedingung
der Bedingung ![]() genügt.
genügt.
Die näherungsweise Berechnung mehrfacher Integrale mit Hilfe der Monte-Carlo-Methode wird am Beispiel des Doppelintegrals
gezeigt. Mit S wird ein ebenes Flächenstück bezeichnet, das durch die Ungleichungen ![]() und
und ![]() beschrieben sein soll. Mit
beschrieben sein soll. Mit ![]() und
und ![]() sind gegebene Funktionen bezeichnet. Dann kann V als Volumen eines zylinderischen Körpers K aufgefaßt werden, der senkrecht auf der x,y-Ebene steht und für dessen Deckfläche
sind gegebene Funktionen bezeichnet. Dann kann V als Volumen eines zylinderischen Körpers K aufgefaßt werden, der senkrecht auf der x,y-Ebene steht und für dessen Deckfläche ![]() gilt. Dieser Körper liege in dem Quader
gilt. Dieser Körper liege in dem Quader ![]() , der durch die Ungleichungen
, der durch die Ungleichungen ![]() beschrieben wird. Nach einer Transformation analog zu (16.179) erhält man aus (16.181) einen Ausdruck, der das Integral
beschrieben wird. Nach einer Transformation analog zu (16.179) erhält man aus (16.181) einen Ausdruck, der das Integral
enthält, wobei V* als Volumen eines Körpers K* im dreidimensionalen Einheitswürfel aufgefaßt werden kann. Das Integral (16.182) wird näherungsweise nach der Monte-Carlo-Methode wie folgt berechnet:
Von einer Folge von Zufallszahlen, die im Intervall [0,1] gleichverteilt sein sollen, faßt man je 3 als Koordinaten eines Punktes ![]() des Einheitswürfels auf und prüft, ob Pi dem Körper K* angehört. Ist das für m Punkte der Fall, dann gilt analog zu (16.175)
des Einheitswürfels auf und prüft, ob Pi dem Körper K* angehört. Ist das für m Punkte der Fall, dann gilt analog zu (16.175)
 |
(16.183) |
Bei bestimmten Integralen mit einer Integratisionsveränderlichen sollte man die im Abschnitt Numerische Integration beschriebenen Verfahren anwenden.
Bei der Berechnung mehrfacher Integrale ist dagegen die Anwendung der Monte-Carlo-Methode durchaus zweckmäßig.