Meßfehlerverteilungsdichte

Spezielle Annahmen über die Eigenschaften der Meßfehler bedingen bestimmte Eigenschaften der Dichtefunktion der Fehlerverteilung:

1. Stetige Dichtefunktion:

Da zufällige Meßfehler beliebige Werte aus einem bestimmten Intervall annehmen können, sind sie durch eine stetige Dichte f(x) zu beschreiben.

2. Gerade Dichtefunktion:

Wenn Meßfehler mit gleichem Absolutbetrag, aber verschiedenem Vorzeichen gleichwahrscheinlich sind, muß die Dichtefunktion eine gerade Funktion sein:
.

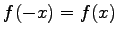3. Monoton fallende Dichtefunktion:

Wenn Meßfehler mit großem Absolutbetrag weniger wahrscheinlich sind als Fehler mit kleinem Absolutbetrag, muß f(x) für x > 0 eine monoton fallende Funktion sein.

4. Endlicher Erwartungswert:

Der Erwartungswert des Absolutbetrages des Fehlers muß eine endliche Größe sein, d.h., es muß gelten:

Durch Zugrundelegung unterschiedlicher Fehlereigenschaften kommt man zu verschiedenen Fehlerdichtefunktionen.