Inhalt Index DeskTop Bronstein
![]()
![]() Wahrscheinlichkeitsrechnung und Mathematische Statistik Wahrscheinlichkeitsrechnung Stetige Verteilungen
Wahrscheinlichkeitsrechnung und Mathematische Statistik Wahrscheinlichkeitsrechnung Stetige Verteilungen
heißt normalverteilt, genauer (![]() )-normalverteilt. Die Funktion
)-normalverteilt. Die Funktion
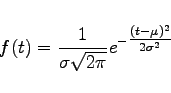 |
(16.71) |
heißt die Dichte der Normalverteilung. Sie nimmt an der Stelle ![]() ihr Maximum an und hat Wendepunkte bei
ihr Maximum an und hat Wendepunkte bei ![]() (s. Abbildung):
(s. Abbildung):
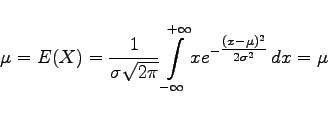 |
(16.72a) |
und
 |
(16.72b) |
Sind die Zufallsveränderlichen X1 und X2 unabhängig und normalverteilt mit den Parametern ![]() bzw.
bzw. ![]() , so ist auch die Zufallsveränderliche
, so ist auch die Zufallsveränderliche ![]() normalverteilt mit den Parametern
normalverteilt mit den Parametern ![]() .
.
Durch die Substitution
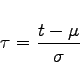
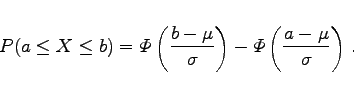 |
(16.73) |
berechnen.