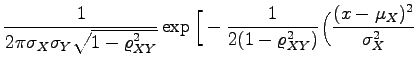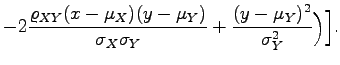Zwei Merkmale X und Y sollen zu einer zweidimensionalen Zufallsgröße (X,Y) mit folgenden Verteilungsfunktionen zusammengefaßt werden:
 |
(16.149a) |
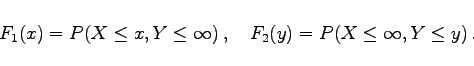 |
(16.149b) |
Die Zufallsgrößen X und Y heißen unabhängig voneinander, wenn
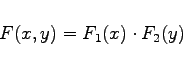 |
(16.150) |
gilt. Die wichtigsten Parameter einer zweidimensionalen Verteilung sind:
- 1. Mittelwerte:
-
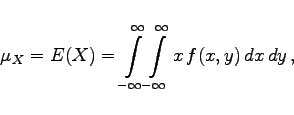 |
(16.151a) |
 |
(16.151b) |
- 2. Streuungen:
-
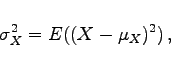 |
(16.152a) |
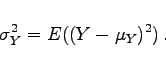 |
(16.152b) |
- 3. Kovarianz:
-
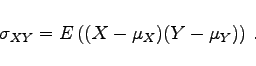 |
(16.153) |
- 4. Korrelationskoeffizient:
-
 |
(16.154) |
Der Korrelationskoeffizient ist ein Maß für die lineare Abhängigkeit von X und Y, denn es gilt: Alle Punkte (X,Y) liegen genau dann mit der Wahrscheinlichkeit 1 auf einer Geraden, wenn  ist. Wenn X und Y unabhängige Zufallsveränderliche sind, dann ist
ist. Wenn X und Y unabhängige Zufallsveränderliche sind, dann ist  . Aus
. Aus  kann man nur dann auf die Unabhängigkeit der Merkmale X und Y schließen, wenn diese einer zweidimensionalen Normalverteilung genügen, die durch die folgende Dichtefunktion definiert ist:
kann man nur dann auf die Unabhängigkeit der Merkmale X und Y schließen, wenn diese einer zweidimensionalen Normalverteilung genügen, die durch die folgende Dichtefunktion definiert ist:
| f(x,y) |
= |
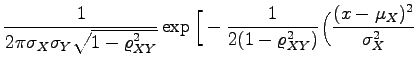 |
|
| |
|
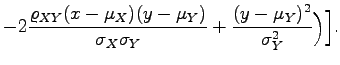 |
(16.155) |
![]()
![]() Wahrscheinlichkeitsrechnung und Mathematische Statistik Mathematische Statistik Korrelation und Regression Lineare Korrelation bei zwei meßbaren Merkmalen
Wahrscheinlichkeitsrechnung und Mathematische Statistik Mathematische Statistik Korrelation und Regression Lineare Korrelation bei zwei meßbaren Merkmalen

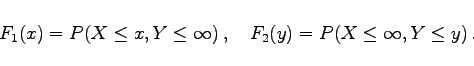
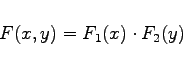
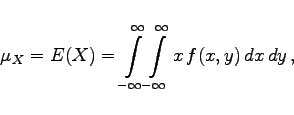

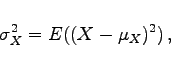
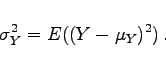
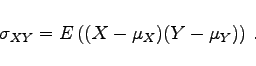

![]() ist. Wenn X und Y unabhängige Zufallsveränderliche sind, dann ist
ist. Wenn X und Y unabhängige Zufallsveränderliche sind, dann ist ![]() . Aus
. Aus ![]() kann man nur dann auf die Unabhängigkeit der Merkmale X und Y schließen, wenn diese einer zweidimensionalen Normalverteilung genügen, die durch die folgende Dichtefunktion definiert ist:
kann man nur dann auf die Unabhängigkeit der Merkmale X und Y schließen, wenn diese einer zweidimensionalen Normalverteilung genügen, die durch die folgende Dichtefunktion definiert ist: