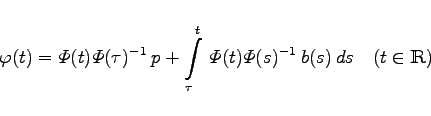Hauptsätze
Es sei A(t)=[aij(t)]i,j=1n eine Matrix-Funktion auf  , wobei jede Komponente
, wobei jede Komponente  als stetige Funktion vorausgesetzt wird, und es sei
als stetige Funktion vorausgesetzt wird, und es sei  eine stetige Vektorfunktion auf
eine stetige Vektorfunktion auf  . Dann heißt
. Dann heißt
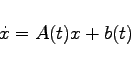 |
(17.13a) |
inhomogene lineare Differentialgleichung erster Ordnung im  und
und
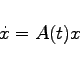 |
(17.13b) |
die zugehörige homogene lineare Differentialgleichung erster Ordnung.
- 1. Hauptsatz über homogene lineare Differentialgleichungen:
- Jede Lösung von (17.13a) existiert auf ganz
 . Die Gesamtheit aller Lösungen von (17.13b) bildet einen n-dimensionalen Untervektorraum LH der C1-glatten Vektorfunktionen über
. Die Gesamtheit aller Lösungen von (17.13b) bildet einen n-dimensionalen Untervektorraum LH der C1-glatten Vektorfunktionen über  .
.
- 2. Hauptsatz über inhomogene lineare Differentialgleichungen:
- Die Gesamtheit aller Lösungen LI von (17.13a) ist ein n-dimensionaler affiner Unterraum der C1-glatten Vektorfunktionen über
 in der Form
in der Form  , wobei
, wobei  eine beliebige Lösung von (17.13a) ist.
eine beliebige Lösung von (17.13a) ist.
Seien  beliebige Lösungen von (17.13b) und
beliebige Lösungen von (17.13b) und  die zugehörige Lösungsmatrix. Dann genügt
die zugehörige Lösungsmatrix. Dann genügt  auf
auf  der Matrix-Differentialgleichung
der Matrix-Differentialgleichung  , wobei
, wobei  ist. Bilden die Lösungen
ist. Bilden die Lösungen  eine Basis von
eine Basis von  , so heißt
, so heißt  Fundamentalmatrix von (17.13b). Bezüglich einer Lösungsmatrix
Fundamentalmatrix von (17.13b). Bezüglich einer Lösungsmatrix  von (17.13b) ist
von (17.13b) ist  die WRONSKI-Determinante. Für sie gilt die Formel von LIOUVILLE:
die WRONSKI-Determinante. Für sie gilt die Formel von LIOUVILLE:
 |
(17.13c) |
Für eine Lösungsmatrix ist  auf
auf  oder
oder  für alle
für alle  . Das System
. Das System  ist also genau dann eine Basis von
ist also genau dann eine Basis von  , wenn
, wenn  für ein t (und damit für alle) ist.
für ein t (und damit für alle) ist.
- 3. Satz über die Variation der Konstanten:
- Sei
 eine beliebige Fundamentalmatrix von (17.13b). Dann läßt sich die Lösung
eine beliebige Fundamentalmatrix von (17.13b). Dann läßt sich die Lösung  von (17.13a) mit Anfang p zur Zeit
von (17.13a) mit Anfang p zur Zeit  in der Form
in der Form
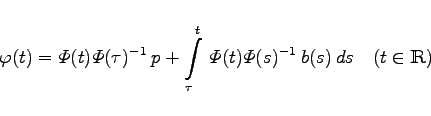 |
(17.13d) |
darstellen.
![]()
![]() Dynamische Systeme und Chaos Gewöhnliche Differentialgleichungen und Abbildungen Qualitative Theorie gewöhnlicher Differentialgleichungen Lineare Differentialgleichungen
Dynamische Systeme und Chaos Gewöhnliche Differentialgleichungen und Abbildungen Qualitative Theorie gewöhnlicher Differentialgleichungen Lineare Differentialgleichungen
![]() , wobei jede Komponente
, wobei jede Komponente ![]() als stetige Funktion vorausgesetzt wird, und es sei
als stetige Funktion vorausgesetzt wird, und es sei ![]() eine stetige Vektorfunktion auf
eine stetige Vektorfunktion auf ![]() . Dann heißt
. Dann heißt![]() und
und
![]() auf
auf ![]() oder
oder ![]() für alle
für alle ![]() . Das System
. Das System ![]() ist also genau dann eine Basis von
ist also genau dann eine Basis von ![]() , wenn
, wenn ![]() für ein t (und damit für alle) ist.
für ein t (und damit für alle) ist.