Inhalt Index DeskTop Bronstein
![]()
![]() Dynamische Systeme und Chaos Gewöhnliche Differentialgleichungen und Abbildungen Dynamische Systeme Invariante Mengen
Dynamische Systeme und Chaos Gewöhnliche Differentialgleichungen und Abbildungen Dynamische Systeme Invariante Mengen
Sei ![]() ein dynamisches System auf dem emtrischen Raum
ein dynamisches System auf dem emtrischen Raum ![]() . Die Menge
. Die Menge ![]() heißt invariant unter
heißt invariant unter ![]() , falls
, falls ![]() für alle
für alle ![]() ist, und positiv invariant unter
ist, und positiv invariant unter ![]() , falls
, falls ![]() für alle
für alle ![]() aus
aus ![]() ist.
ist.
Für jedes ![]() ist die
ist die ![]() -Grenzmenge des Orbits durch x die Menge
-Grenzmenge des Orbits durch x die Menge
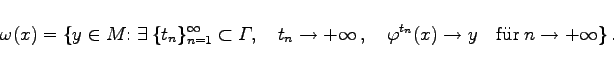 |
(17.7) |
Die Elemente von ![]() heißen
heißen ![]() -Grenzpunkte des Orbits. Liegt ein invertierbares dynamisches System vor, so heißt für jedes
-Grenzpunkte des Orbits. Liegt ein invertierbares dynamisches System vor, so heißt für jedes ![]() die Menge
die Menge
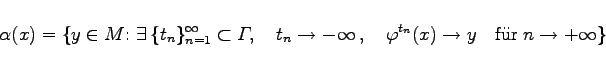 |
(17.8) |
![]() -Grenzmenge des Orbits durch x; die Elemente von
-Grenzmenge des Orbits durch x; die Elemente von ![]() heißen
heißen ![]() -Grenzpunkte des Orbits.
-Grenzpunkte des Orbits.
Die lokale Eigenschaft des Volumenschrumpfens führt bei vielen Systemen zur Existenz einer beschränkten Menge im Phasenraum, in die alle Orbits für wachsende Zeiten gelangen und dort verbleiben. Eine beschränkte, offene und zusammenhängende Menge ![]() heißt absorbierend bezüglich
heißt absorbierend bezüglich ![]() , falls
, falls ![]() für alle positiven t aus
für alle positiven t aus ![]() ist. (
ist. (![]() ist die Abschließung von
ist die Abschließung von ![]() .)
.)
| Beispiel |
|
Gegeben sei in der Ebene das Differentialgleichungssystem |
Unter Verwendung von Polarkoordinaten ![]() läßt sich die Lösung von (17.9a) mit Anfang
läßt sich die Lösung von (17.9a) mit Anfang ![]() zur Zeit t = 0 in der Form
zur Zeit t = 0 in der Form
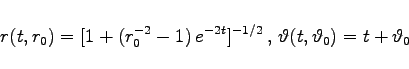 |
(17.9b) |
schreiben. Aus dieser Lösungsdarstellung folgt, daß der Fluß von (17.9a) einen ![]() -periodischen Orbit besitzt, der als
-periodischen Orbit besitzt, der als ![]() dargestellt werden kann. Für die Grenzmengen der Orbits durch p gilt
dargestellt werden kann. Für die Grenzmengen der Orbits durch p gilt
