Inhalt Index DeskTop Bronstein
![]()
![]() Optimierung Nichtlineare Optimierung Gradientenverfahren für Probleme mit Ungleichungsrestriktionen Verfahren der zulässigen Richtungen
Optimierung Nichtlineare Optimierung Gradientenverfahren für Probleme mit Ungleichungsrestriktionen Verfahren der zulässigen Richtungen
Eine zulässige Abstiegsrichtung ![]() im Punkt
im Punkt ![]() kann durch Lösung des folgenden Optimierungsproblems gewonnen werden:
kann durch Lösung des folgenden Optimierungsproblems gewonnen werden:
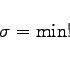 |
(18.96) |
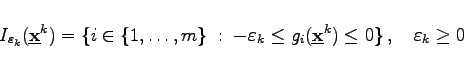 |
(18.98) |
der sogenannten in ![]()
![]() -aktiven Restriktionen ersetzt wird. Dadurch werden lokal Abstiegsrichtungen ausgeschlossen, die von
-aktiven Restriktionen ersetzt wird. Dadurch werden lokal Abstiegsrichtungen ausgeschlossen, die von ![]() ausgehend näher an den von
ausgehend näher an den von ![]() -aktiven Restriktionen gebildeten Rand von M heranführen (s. Abbildung).
-aktiven Restriktionen gebildeten Rand von M heranführen (s. Abbildung).
Ist nach dieser Modifizierung ![]() Lösung von (18.97a,b,c), dann ist
Lösung von (18.97a,b,c), dann ist ![]() nur dann ein stationärer Punkt, wenn
nur dann ein stationärer Punkt, wenn ![]() erfüllt ist. Anderenfalls ist
erfüllt ist. Anderenfalls ist ![]() geeignet zu verkleinern und das Richtungssuchprogramm zu wiederholen (s. [18.6]).
geeignet zu verkleinern und das Richtungssuchprogramm zu wiederholen (s. [18.6]).