Inhalt Index DeskTop Bronstein
![]()
![]() Optimierung Lineare Optimierung Grundbegriffe der linearen Optimierung, Normalform Normalform der linearen Optimierungsaufgabe
Optimierung Lineare Optimierung Grundbegriffe der linearen Optimierung, Normalform Normalform der linearen Optimierungsaufgabe
Ist eine Ecke von M bekannt, dann kann eine Normalform des linearen Optimierungsproblems wie folgt ermittelt werden. Man wählt eine zur Ecke gehörende Basis aus m Spalten von ![]() Im Normalfall sind diese Spalten durch die positiven Komponenten der Ecke festgelegt. Die Basisvariablen werden zum Vektor
Im Normalfall sind diese Spalten durch die positiven Komponenten der Ecke festgelegt. Die Basisvariablen werden zum Vektor ![]() und die Nichtbasisvariablen zum Vektor
und die Nichtbasisvariablen zum Vektor ![]() zusammengefaßt. Die zur Basis gehörenden Spalten bilden die Basismatrix A
zusammengefaßt. Die zur Basis gehörenden Spalten bilden die Basismatrix A![]() , die restlichen Spalten die Matrix
, die restlichen Spalten die Matrix ![]() Dann gilt
Dann gilt
Die Matrix ![]() ist regulär und besitzt die Inverse
ist regulär und besitzt die Inverse ![]() die sogenannte Basisinverse. Multiplikation von (18.9) mit
die sogenannte Basisinverse. Multiplikation von (18.9) mit ![]() und Umstellung der Zielfunktion nach den Nichbasisvariablen liefert eine kanonische Form des Linearen Optimierungsproblems:
und Umstellung der Zielfunktion nach den Nichbasisvariablen liefert eine kanonische Form des Linearen Optimierungsproblems:
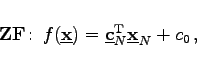 |
(18.10a) |
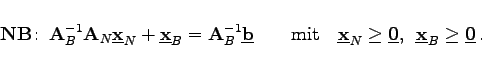 |
(18.10b) |
| Beispiel |
|
Im obigen Beispiel ist |
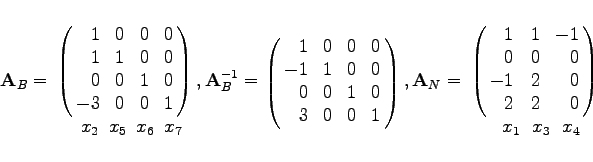 |
(18.11a) |
und
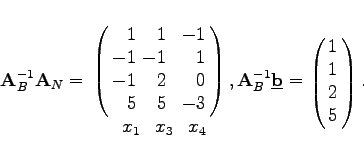 |
(18.11b) |
Es ergibt sich das System
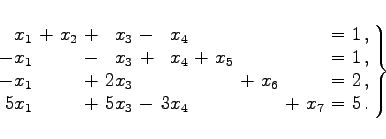 |
(18.12) |
Aus ![]() erhält man durch Subtraktion der mit 3 multiplizierten ersten Nebenbedingung eine auf Nichtbasisvariablen umgerechnete Zielfunktion
erhält man durch Subtraktion der mit 3 multiplizierten ersten Nebenbedingung eine auf Nichtbasisvariablen umgerechnete Zielfunktion
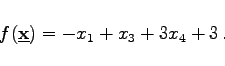 |
(18.13) |