Nichtentarteter Fall

Ist ein Tableau nicht entscheidbar (Fall c), dann wird ein neues Tableau bestimmt, indem eine Basisvariable x_p ausgewählt und gegen eine Nichtbasisvariable x_q ausgetauscht wird:

Schema 3

Dabei sind folgende Austauschregeln zu beachten:

= (18.15a)

= (18.15b)

= (18.15c) =

= (18.15d)

Das Element a_pq heißt Pivotelement, die p-te Zeile Pivotzeile und die q-te Spalte Pivotspalte. Bei der Auswahl von Pivotzeile und Pivotspalte sind zwei Bedingungen zu berücksichtigen:

1. Das neue Tableau muß zulässig sein, d.h., es muß gelten .
2. Es muß gelten .

Dann ist eine neue Ecke mit nicht kleinerem Zielfunktionswert . Die angegebenen Bedingungen werden mit der folgenden Wahl des Pivotelementes erfüllt:

1. Wähle ein q mit c_q > 0 als Pivotspalte.
2. Wähle die Pivotzeile p so, daß gilt:

Sind die Ecken des zulässigen Bereiches nicht entartet, dann bricht das Simplexverfahren nach einer endlichen Anzahl von Simplexschritten mit einem entscheidbaren Tableau ab (Fall a) oder Fall b)).

Beispiel

Die zum Beispiel unter Ecke und Basis gefundene Normalform kann direkt in ein Simplextableau übertragen werden.

Schema 4a, b
 

Das Tableau ist nicht optimal, da in der letzten Zeile noch positive Koeffizienten der Zielfunktion auftreten. Die dritte Spalte wird als Pivotspalte festgelegt (auch die zweite Spalte wäre denkbar). Mit allen positiven Koeffizienten der Pivotspalte bildet man die Quotienten . Die Quotienten wurden hinter der letzten Spalte des Tableaus notiert. Der kleinste Quotient legt die Pivotzeile fest. Ist die Pivotzeile nicht eindeutig zu bestimmen, dann ist die durch das neue Tableau bestimmte Ecke entartet. Mit den Austauschregeln erhält man das rechte Tableau. Dieses Tableau bestimmt die Ecke , die dem Punkt P₇ in der Abbildung entspricht.

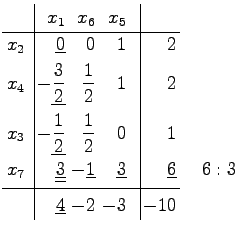
Da das neue Tableau nicht optimal ist, wird jetzt x₆ gegen x₃ getauscht (nächstes linkes Schema). Die Ecke des 3. Tableaus entspricht dem Punkt P₆ in der Abbildung. Nach einem weiteren Tausch erhält man ein optimales Tableau (nächstes rechtes Schema) mit dem Maximalpunkt , der dem Punkt P₅ mit dem maximalen Zielfunktionswert entspricht.

Schema 4c, d