Fallunterscheidung

Ziel der Lösung des Hilfsprogramms mit dem Simplexverfahren ist es, die künstlichen Variablen aus der Basis zu entfernen. Wird eine künstliche Variable zur Nichtbasisvariable, dann kann die zugehörige Spalte im Tableau gestrichen werden. Man ermittelt so einen Maximalpunkt und unterscheidet:

1. :

Das System besitzt keine Lösung.

2. :

Falls sich unter den Basisvariablen keine künstlichen Variablen befinden, ist sofort ein Tableau für die ursprüngliche Aufgabe gegeben. Anderenfalls wird so lange aus einer zu einer künstlichen Variablen gehörenden Zeile ein Pivotelement gewählt, ein Austauschschritt ausgeführt und anschließend die Pivotspalte gestrichen, bis alle künstlichen Variablen aus dem Tableau entfernt worden sind.

Durch die Einführung von künstlichen Variablen kann die Dimension des Hilfsproblems stark anwachsen. Mitunter ist es nicht notwendig, zu jeder Gleichung eine künstliche Variable zu addieren. War das System der Nebenbedingungen vor der Einführung von Schlupfvariablen gegeben durch
mit , dann sind nur in den ersten beiden Systemen künstliche Variable erforderlich. Für das dritte System können die Schlupfvariablen als erste Basisvariable gewählt werden.

Beispiel

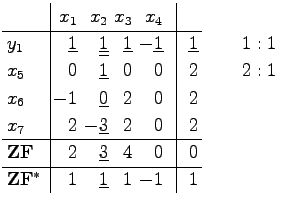
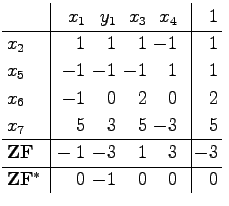
Im Beispiel unter Ecke und Basis ist nur in der ersten Gleichung eine künstliche Variable erforderlich:

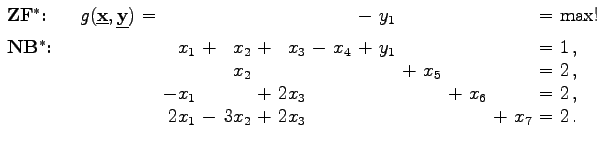Das ermittelte Tableau ist mit optimal. Durch Streichen der zweiten Spalte erhält man ein erstes Tableau für das Ausgangsproblem.
Schema 6a, b