Revidierter Simplexschritt

1. Das Tableau ist nicht optimal, solange wenigstens ein c_j > 0 ist .
   Auswahl der Pivotspalte q für ein .
2. Berechnung der Pivotspalte durch Multiplikation der q-ten Spalte der Koeffizientenmatrix von (18.18b) mit und Eintragen des ermittelten Vektors in die letzte Spalte des Tableaus.
   Ermittlung der Pivotzeile wie beim Simplexalgorithmus gemäß (18.16).
3. Berechnung des neuen Tableaus mit den Austauschregeln (18.15a-d), wobei formal a_iq durch r_i ersetzt wird und die Indizes im Bereich liegen. Die Größen werden nicht eingetragen. Mit ermittelt man für , wobei die j-te Spalte der Koeffizientenmatrix von (18.18b) darstellt.

Beispiel

In die Normalform des unter Ecke und Basis behandelten Beispiels soll x₄ aufgenommen werden. Die zugehörige Pivotspalte wird in das folgende linke Tableau eingetragen.

Schema 8a, b
    

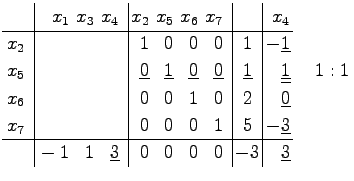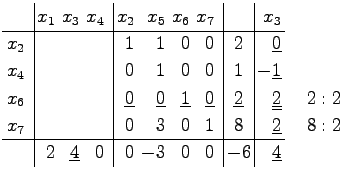Für j = 1, 3, 4 erhält man :     .

Der ermittelte Eckpunkt entspricht dem Punkt P₇ in der Abbildung aus dem betrachteten Beispiel.

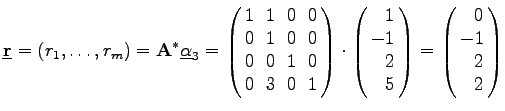Als nächste Pivotspalte wird j = 3 bestimmt. Die Größe mit

ist im rechten Tableau bereits eingetragen. Der weitere Rechengang erfolgt in Analogie zum Beispiel im Abschnitt Übergang zum neuen Simplextableau, nichtentarteter Fall.