- 1. Aufgabenstellung:
- Es sei f auf [a,b] unimodal und x* ein globaler Minimalpunkt. Dann soll ein Intervall
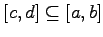 mit
mit 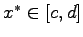 und
und 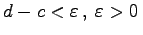 , bestimmt werden. Dabei heißt
, bestimmt werden. Dabei heißt 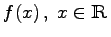 , eine unimodale Funktion im Intervall
, eine unimodale Funktion im Intervall 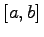 , falls f auf jedem abgeschlossenen Teilintervall
, falls f auf jedem abgeschlossenen Teilintervall 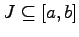 genau einen lokalen Minimalpunkt besitzt.
genau einen lokalen Minimalpunkt besitzt.
- 2. Gleichmäßige Suche:
- Man wählt n (n ganzzahlig) so, daß
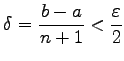 gilt, und berechnet die Werte f(xk) für
gilt, und berechnet die Werte f(xk) für 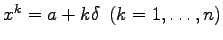 . Ist f(x) unter diesen Funktionswerten ein kleinster Wert, dann liegt der Minimalpunkt x* im Intervall
. Ist f(x) unter diesen Funktionswerten ein kleinster Wert, dann liegt der Minimalpunkt x* im Intervall 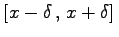 . Die für die geforderte Genauigkeit notwendige Anzahl von Funktionswertberechnungen kann mittels
. Die für die geforderte Genauigkeit notwendige Anzahl von Funktionswertberechnungen kann mittels
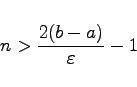 |
(18.66) |
abgeschätzt werden.
![]()
![]() Optimierung Nichtlineare Optimierung Numerische Suchverfahren Eindimensionale Suche
Optimierung Nichtlineare Optimierung Numerische Suchverfahren Eindimensionale Suche
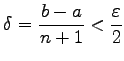 gilt, und berechnet die Werte f(xk) für
gilt, und berechnet die Werte f(xk) für