Numerische Integration

Die Berechnung bestimmter Integrale ist oft nur numerisch möglich. Das ist der Fall, wenn der Integrand sehr kompliziert aufgebaut ist bzw. wenn die Stammfunktion nicht durch elementare Funktionen ausdrückbar ist. In Maple wird dann der Befehl dem Integrationsbefehl für die Berechnung des bestimmten Integrals vorangestellt:

Darauf wird das Integral mit der geforderten Genauigkeit von Maple unter Zuhilfenahme von Näherungsverfahren bestimmt. In der Regel funktioniert diese Methode.

Beispiel

Berechnung des bestimmten Integrals 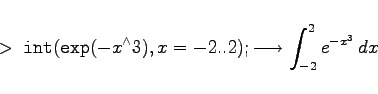. Da die Stammfunktion nicht bekannt ist, wird zunächst

angezeigt. Gibt man jedoch

ein, so erhält man 277.745841695583. Maple hat unter Benutzung des eingebauten Näherungsverfahrens die numerische Integration auf 15 Ziffern genau vorgenommen.

In gewissen Fällen versagt diese Methode, insbesondere wenn über große Intervalle zu integrieren ist. Dann kann man versuchen, mit dem Bibliotheksaufruf

eine andere Näherungsprozedur aufzurufen, die ein adaptives Newtonverfahren verwendet.

Beispiel

Die Eingabe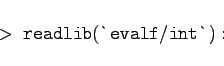

führt zu einer Fehlermeldung. Mit

erhält man das richtige Resultat. Hier ist das dritte Argument die Angabe der Genauigkeit und das letzte die interne Bezeichnung des Näherungsverfahrens.