Hyperbelkosinus

Der Hyperbelkosinus (2.156) ist eine gerade Funktion, die für x < 0 von auf 1 monoton fällt und für x > 0 von 1 bis monoton wächst.

Das Minimum liegt bei . Asymptoten gibt es keine. Die Kurve verläuft symmetrisch bezüglich der y-Achse und bleibt mit ihren Werten oberhalb der quadratischen Parabel 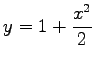(schwarz gezeichnete Kurve). Da die Funktion eine Kettenlinie beschreibt, nennt man die Kurve auch Katenoide.