Parabel n-ter Ordnung

Die Funktion

y=axⁿ (2.44)

mit 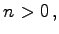ganzzahlig, liefert als Kurve eine Parabel n-ter Ordnung.

Spezialfall :

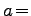
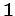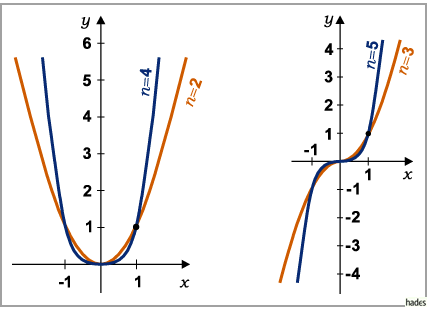
Die Kurve y = xⁿ geht durch die Punkte (0,0) und (1,1) und berührt oder schneidet die x-Achse im Koordinatenursprung. Für gerades n ergibt sich eine zur y-Achse symmetrische Kurve mit einem Minimum im Koordinatenursprung. Für ungerades n ergibt sich eine zentralsymmetrische Kurve zum Koordinatenursprung, der zugleich Wendepunkt ist. Asymptoten gibt es keine.

Allgemeiner Fall a:

Man erhält die Kurve y = axⁿ aus der zu y = xⁿ gehörenden Kurve durch Streckung der Abszissen mit dem Faktor 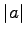. Für a < 0 spiegelt man y = |a|xⁿ an der x-Achse.