Inhalt Index DeskTop Bronstein
![]()
![]() Funktionen und ihre Darstellung Gebrochenrationale Funktionen
Funktionen und ihre Darstellung Gebrochenrationale Funktionen
Die Funktion
beschreibt eine Kurve 3. Ordnung, die symmetrisch zu der vertikalen Geraden bei  verläuft und die die x-Achse zur Asymptote hat.
verläuft und die die x-Achse zur Asymptote hat.
Ihr Verhalten hängt von den Vorzeichen von a und ![]() ab. Von den zwei Fällen a > 0 und a < 0 wird hier nur der erste betrachtet, da der zweite durch Spiegelung von
ab. Von den zwei Fällen a > 0 und a < 0 wird hier nur der erste betrachtet, da der zweite durch Spiegelung von  an der x-Achse erhalten werden kann.
an der x-Achse erhalten werden kann.
 die Wendepunkte B und C liegen bei
die Wendepunkte B und C liegen bei  die zugehörigen Tangentensteigungen (Richtungskoeffizienten) berechnen sich zu
die zugehörigen Tangentensteigungen (Richtungskoeffizienten) berechnen sich zu 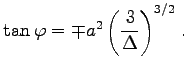
 eine Unstetigkeitsstelle mit
eine Unstetigkeitsstelle mit  ; die Unstetigkeitsstellen liegen bei
; die Unstetigkeitsstellen liegen bei  .
.