Exponentialsumme
Die Funktion
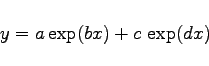 |
(2.60) |
ist in den folgenden vier Abbildungen für charakteristische Vorzeichen-Relationen dargestellt.
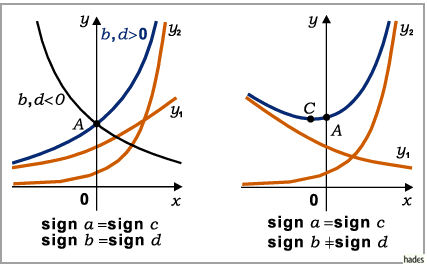
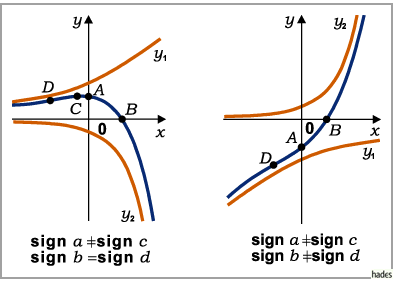
Die Konstruktion der Kurve erfolgt über die Addition der Ordinaten der Kurven der beiden Summanden y1 = aebx und 
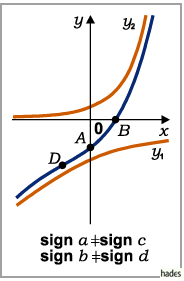
Die Funktion ist stetig. Wenn keine der Zahlen a, b, c, d gleich 0 ist, besitzt die Kurve eine der vier dargestellten Formen. Die Kurvenbilder können in Abhängigkeit von den Vorzeichen der Parameter an den Koordinatenachsen gespiegelt sein.
Die Schnittpunkte A und B mit der y- bzw. x-Achse liegen bei (0,a+c) bzw. 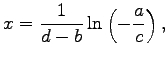 das Extremum C bei
das Extremum C bei  und der Wendepunkt D bei
und der Wendepunkt D bei  soweit diese Punkte vorhanden sind.
soweit diese Punkte vorhanden sind.
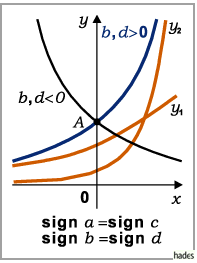
- Fall a)
- Die Parameter a und c bzw. b und d besitzen gleiches Vorzeichen: Die Funktion erfährt keinen Vorzeichenwechsel; sie ändert sich von 0 bis
 bzw.
bzw.  oder von
oder von  bzw.
bzw.  bis 0. Wendepunkte gibt es keine; Asymptote ist die x-Achse.
bis 0. Wendepunkte gibt es keine; Asymptote ist die x-Achse.
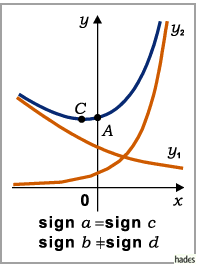
- Fall b)
- Die Parameter a und c haben gleiche, b und d verschiedene Vorzeichen: Die Funktion ändert sich ohne Vorzeichenwechsel von
 bis
bis  wobei sie ein Minimum durchläuft, bzw. von
wobei sie ein Minimum durchläuft, bzw. von  bis
bis  , dabei ein Maximum durchlaufend. Wendepunkte gibt es keine.
, dabei ein Maximum durchlaufend. Wendepunkte gibt es keine.
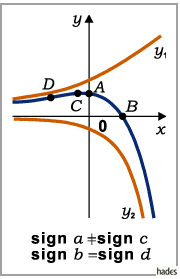
- Fall c)
- Die Parameter a und c haben verschiedene, b und d gleiche Vorzeichen: Die Funktion ändert sich von 0 bis
 bzw.
bzw.  oder von
oder von  bzw.
bzw.  bis 0, wobei sie einmal ihr Vorzeichen wechselt und ein Extremum C und einen Wendepunkt D durchläuft. Die x-Achse ist Asymptote.
bis 0, wobei sie einmal ihr Vorzeichen wechselt und ein Extremum C und einen Wendepunkt D durchläuft. Die x-Achse ist Asymptote.
- Fall d)
- Die Parameter a und c und auch b und d besitzen unterschiedliche Vorzeichen: Die Funktion ändert sich monoton zwischen
 und
und  bzw. zwischen
bzw. zwischen  und
und  . Sie besitzt keine Extrema, aber einen Wendepunkt
. Sie besitzt keine Extrema, aber einen Wendepunkt 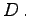
![]()
![]() Funktionen und ihre Darstellung Exponentialfunktionen und logarithmische Funktionen
Funktionen und ihre Darstellung Exponentialfunktionen und logarithmische Funktionen
![]()
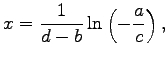 das Extremum C bei
das Extremum C bei  und der Wendepunkt D bei
und der Wendepunkt D bei  soweit diese Punkte vorhanden sind.
soweit diese Punkte vorhanden sind.