Da die trigonometrischen Funktionen periodisch sind (Periode  bzw.
bzw.  ), kann die Ermittlung der Funktionswerte für beliebige Argumentwerte x nach den folgenden Regeln vereinfacht werden:
), kann die Ermittlung der Funktionswerte für beliebige Argumentwerte x nach den folgenden Regeln vereinfacht werden:
Argument x mit x  bzw. x
bzw. x  : Wenn der Winkel x größer als
: Wenn der Winkel x größer als  (bzw. größer als
(bzw. größer als  ) ist, dann werden die Werte der trigonometrischen Funktionen auf Funktionswerte für Winkel
) ist, dann werden die Werte der trigonometrischen Funktionen auf Funktionswerte für Winkel  mit
mit  (bzw.
(bzw.  ) nach folgenden Regeln zurückgeführt (n ganzzahlig):
) nach folgenden Regeln zurückgeführt (n ganzzahlig):
 |
(2.69a) |
 |
(2.69b) |
 |
(2.69c) |
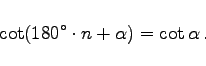 |
(2.69d) |
Argument x mit x < 0: Wenn das Argument negativ ist ( ), dann werden die Funktionen mit den folgenden Formeln auf Funktionen mit positivem Argument zurückgeführt:
), dann werden die Funktionen mit den folgenden Formeln auf Funktionen mit positivem Argument zurückgeführt:
 |
(2.70a) |
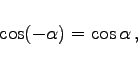 |
(2.70b) |
 |
(2.70c) |
 |
(2.70d) |
Argument x mit  x
x  : Wenn
: Wenn  ist, dann werden die Funktionen mit Hilfe der Reduktionsformeln auf Funktionen eines spitzen Winkels
ist, dann werden die Funktionen mit Hilfe der Reduktionsformeln auf Funktionen eines spitzen Winkels  zurückgeführt. Man nennt die Beziehungen zwischen Funktionswerten von Winkeln, die sich um
zurückgeführt. Man nennt die Beziehungen zwischen Funktionswerten von Winkeln, die sich um  oder
oder  unterscheiden bzw. zu
unterscheiden bzw. zu  oder
oder  ergänzen, Quadrantenrelationen.
ergänzen, Quadrantenrelationen.
Tabelle Reduktionsformeln oder Quadrantenrelationen der trigonometrischen Funktionen
Aus der 1. und 2. Spalte ergeben sich die Formeln der Komplementsätze, aus der 1. und 3. die Formeln der Supplementsätze. Da  der Komplementwinkel oder das Komplement von
der Komplementwinkel oder das Komplement von  ist, nennt man Beziehungen der Art
ist, nennt man Beziehungen der Art
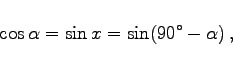 |
(2.71a) |
 |
(2.71b) |
Komplementsätze.
Die Beziehungen zwischen den trigonometrischen Funktionen für Supplementwinkel der Art
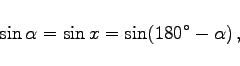 |
(2.72a) |
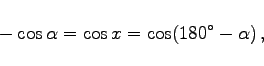 |
(2.72b) |
werden wegen  Supplementsätze genannt.
Supplementsätze genannt.
Argument x mit  x
x  : Wenn ein spitzer Winkel
: Wenn ein spitzer Winkel  vorliegt, dann wurden die Funktionswerte früher Tabellen entnommen; heute werden sie vom Rechner abgefragt.
vorliegt, dann wurden die Funktionswerte früher Tabellen entnommen; heute werden sie vom Rechner abgefragt.
| Beispiel |
|
 . .
|
![]()
![]() Funktionen und ihre Darstellung Trigonometrische Funktionen (Winkelfunktionen) Grundlagen Wertebereiche und Funktionsverläufe der trigonometrischen Funktionen
Funktionen und ihre Darstellung Trigonometrische Funktionen (Winkelfunktionen) Grundlagen Wertebereiche und Funktionsverläufe der trigonometrischen Funktionen
![]() bzw.
bzw. ![]() ), kann die Ermittlung der Funktionswerte für beliebige Argumentwerte x nach den folgenden Regeln vereinfacht werden:
), kann die Ermittlung der Funktionswerte für beliebige Argumentwerte x nach den folgenden Regeln vereinfacht werden:![]() bzw. x
bzw. x ![]() : Wenn der Winkel x größer als
: Wenn der Winkel x größer als ![]() (bzw. größer als
(bzw. größer als ![]() ) ist, dann werden die Werte der trigonometrischen Funktionen auf Funktionswerte für Winkel
) ist, dann werden die Werte der trigonometrischen Funktionen auf Funktionswerte für Winkel ![]() mit
mit ![]() (bzw.
(bzw. ![]() ) nach folgenden Regeln zurückgeführt (n ganzzahlig):
) nach folgenden Regeln zurückgeführt (n ganzzahlig):


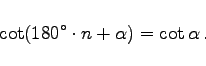
![]() ), dann werden die Funktionen mit den folgenden Formeln auf Funktionen mit positivem Argument zurückgeführt:
), dann werden die Funktionen mit den folgenden Formeln auf Funktionen mit positivem Argument zurückgeführt:
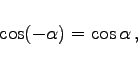


![]() x
x ![]() : Wenn
: Wenn ![]() ist, dann werden die Funktionen mit Hilfe der Reduktionsformeln auf Funktionen eines spitzen Winkels
ist, dann werden die Funktionen mit Hilfe der Reduktionsformeln auf Funktionen eines spitzen Winkels ![]() zurückgeführt. Man nennt die Beziehungen zwischen Funktionswerten von Winkeln, die sich um
zurückgeführt. Man nennt die Beziehungen zwischen Funktionswerten von Winkeln, die sich um ![]() oder
oder ![]() unterscheiden bzw. zu
unterscheiden bzw. zu ![]() oder
oder ![]() ergänzen, Quadrantenrelationen.
ergänzen, Quadrantenrelationen.![]() der Komplementwinkel oder das Komplement von
der Komplementwinkel oder das Komplement von ![]() ist, nennt man Beziehungen der Art
ist, nennt man Beziehungen der Art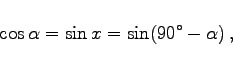

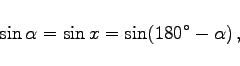
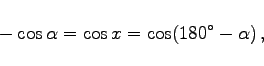
![]() Supplementsätze genannt.
Supplementsätze genannt.![]() x
x ![]() : Wenn ein spitzer Winkel
: Wenn ein spitzer Winkel ![]() vorliegt, dann wurden die Funktionswerte früher Tabellen entnommen; heute werden sie vom Rechner abgefragt.
vorliegt, dann wurden die Funktionswerte früher Tabellen entnommen; heute werden sie vom Rechner abgefragt.