Faktorzerlegung von Polynomen

Maple ist in der Lage Polynome über algebraischen Erweiterungskörpern zu zerlegen, sofern es prinzipiell möglich ist.

Beispiel

Zunächst hat Maple eine Faktorzerlegung der beiden Polynome in irreduzible Faktoren bezüglich des Körpers der rationalen Zahlen durchgeführt. Will man eine weitere Zerlegung über einem algebraischen Erweiterungskörper, so ist folgendermaßen vorzugehen:

Beispiel

Maple hat den zweiten Faktor weiter zerlegt (in diesem Fall nach einer formalen Erweiterung des Körpers mit ).

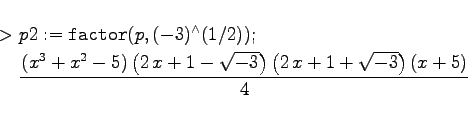In der Regel weiß man nicht, ob eine solche Erweiterung möglich ist. Sind die Grade der gefundenen Faktoren , so ist dies immer möglich. Mit der Operation lassen sich dann die Wurzeln als algebraische Ausdrücke darstellen.

Beispiel

Der Aufruf von k[3] ergibt den konjugiert komplexen Wert von k[2].

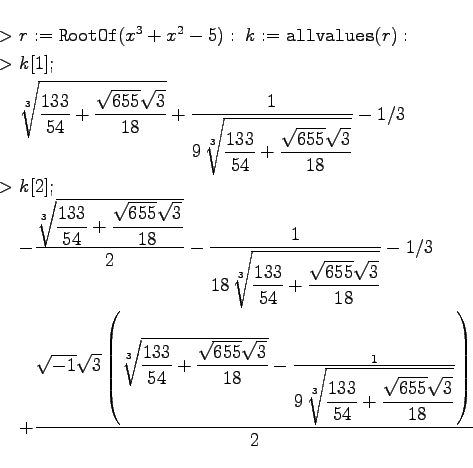Die in diesem Beispiel beschriebene Prozedur liefert im Falle eines Polynoms, das nur über dem Körper der reellen oder komplexen Zahlen reduzibel ist, eine Folge der Wurzeln als Gleitpunktzahlen.