|
Ein Quantensystem besitze drei Energieniveaus der Energien  ,  und  , wobei  eine für dieses System charakteristische Kreisfrequenz und 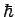 das PLANCKsche Wirkungsquantum ist. Die zu den Energien gehörigen Zustandsvektoren (siehe Zustände und Observable)  ,  und  bilden eine Orthonormalbasis des HILBERT-Raumes  . Der Projektor auf den i-ten Energieeigenzustand ist folglich gegeben durch  . Die Spektraldarstellung des Energie- bzw. HAMILTON-Operators (vegleiche das Beispiel Meßprozeß bei reinen Zuständen) lautet damit:
Die Darstellung der Eigenvektoren als Spaltenvektoren  ,  bzw.  ergibt für die Projektoren 
 |
(21.32) |
und analog
 sowie |
(21.33) |
Für die Spektralzerlegung von  in Matrixdarstellung bezüglich der Orthonormalbasis der Eigenvektoren  folgt schließlich dessen Diagonalform:
 |
(21.34) |
|
Mathematische Grundlagen der Quantenmechanik Mathematischer Rahmen Lineare Operatoren
besitzt eine Spektralzerlegung [23.1]. Im endlichdimensionalen Fall lautet sie:
die Eigenwerte, und 
bezeichnen. Es gilt:
