Inhalt Index DeskTop Bronstein
![]()
![]() Mathematische Grundlagen der Quantenmechanik Mathematischer Rahmen Lineare Operatoren
Mathematische Grundlagen der Quantenmechanik Mathematischer Rahmen Lineare Operatoren
Sei ![]() ein endlichdimensionaler HILBERT-Raum mit den Basisvektoren
ein endlichdimensionaler HILBERT-Raum mit den Basisvektoren ![]() , welche der Orthonormalitätsbedingung
, welche der Orthonormalitätsbedingung ![]() genügen. Hierbei bezeichnet
genügen. Hierbei bezeichnet ![]() das KRONECKER-Symbol, welches durch
das KRONECKER-Symbol, welches durch ![]() für
für ![]() und
und ![]() für
für ![]() definiert ist.
definiert ist.
Ein linearer Operator ![]() ist dann durch die Matrix
ist dann durch die Matrix
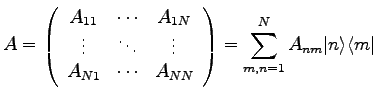 |
(21.11) |
 |
(21.13) |
 |
(21.14) |