Ein Quantenregister besteht aus ![]() Qubits,
Qubits, ![]() . Sein HILBERT-Raum
. Sein HILBERT-Raum 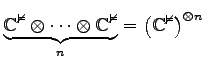 ist das
ist das ![]() -fache Tensorprodukt von
-fache Tensorprodukt von ![]() , hat also die Dimension
, hat also die Dimension ![]() . Ein Zustandsvektor im Quantenregister hat die allgemeine Form
. Ein Zustandsvektor im Quantenregister hat die allgemeine Form
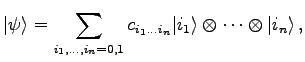 |
(22.8) |
| Beispiel Drei Qubits (n = 3) |
|
Der HILBERT-Raum hat die Dimension 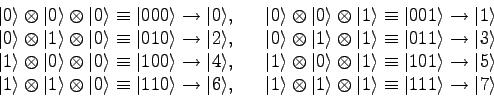 |