Inhalt Index DeskTop Bronstein
![]()
![]() Geometrie Sphärische Trigonometrie Grundbegriffe der Geometrie auf der Kugel
Geometrie Sphärische Trigonometrie Grundbegriffe der Geometrie auf der Kugel
Durch die Endpunkte A und B eines Kugeldurchmessers sollen zwei Ebenen ![]() und
und ![]() verlaufen, die den Winkel
verlaufen, die den Winkel ![]() miteinander einschließen und zwei Großkreishälften
miteinander einschließen und zwei Großkreishälften ![]() und
und ![]() definieren.
definieren.
Der von zwei Großkreishälften begrenzte Teil der Kugeloberfläche wird sphärisches Zweieck oder Kugelzweieck genannt. Als Seiten des sphärischen Zweiecks werden die sphärischen Abstände zwischen den Punkten A und B auf den Großkreisen definiert. Jede Seite beträgt daher ![]()
Als Winkel des sphärischen Zweiecks werden die Winkel zwischen den Tangenten an die Großkreise g1 und g2 in den Punkten A und B definiert. Sie sind gleich und stimmen mit dem sogenannten Keilwinkel ![]() zwischen den Ebenen
zwischen den Ebenen ![]() und
und ![]() überein. Sind C und D die Halbierungspunkte der beiden Großkreisbogen durch A und B, dann kann der Winkel
überein. Sind C und D die Halbierungspunkte der beiden Großkreisbogen durch A und B, dann kann der Winkel ![]() auch als sphärischer Abstand der Punkte C und D aufgefaßt werden. Die Fläche Az des Kugelzweiecks verhält sich zur Kugelfläche wie der Winkel
auch als sphärischer Abstand der Punkte C und D aufgefaßt werden. Die Fläche Az des Kugelzweiecks verhält sich zur Kugelfläche wie der Winkel ![]() zu
zu ![]() Daraus folgt
Daraus folgt
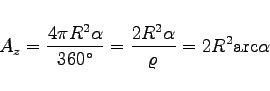 |
(3.182) |
mit dem Umrechnungsfaktor ![]() gemäß (3.179c).
gemäß (3.179c).