3. Grundaufgabe SWS
Gegeben: 2 Seiten und der eingeschlossene Winkel, z. B. 
Bedingungen: Keine.

1. Lösung: Gesucht c bzw. c und 
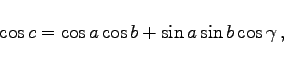 |
(3.213a) |
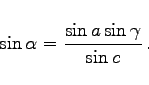 |
(3.213b) |
 kann im I. oder II. Quadranten liegen. Zwei Entscheidungsmöglichkeiten:
kann im I. oder II. Quadranten liegen. Zwei Entscheidungsmöglichkeiten:
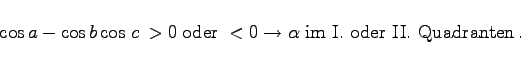 |
(3.214) |
2. Lösung: Gesucht  bzw.
bzw.  und
und 
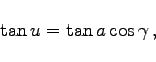 |
(3.215a) |
 |
(3.215b) |
 |
(3.215c) |
3. Lösung: Gesucht  und (oder)
und (oder) 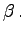
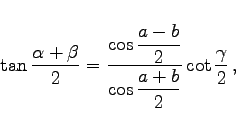 |
(3.216a) |
 |
(3.216b) |
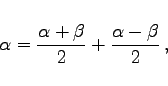 |
(3.216c) |
 |
(3.216d) |
4. Lösung: Gesucht  Ausgangspunkt ist die Verwendung der Neperschen Gleichungen (3.204a) und (3.204b).
Ausgangspunkt ist die Verwendung der Neperschen Gleichungen (3.204a) und (3.204b).
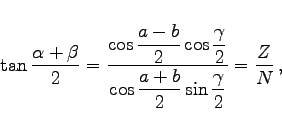 |
(3.217a) |
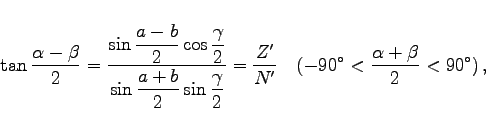 |
(3.217b) |
 |
(3.217c) |
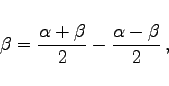 |
(3.217d) |
 |
(3.217e) |
 |
(3.217f) |
Probe: Doppelte Berechnung von 
Hinweis: Die Lösung der 3. Grundaufgabe kann auch durch Zerlegung des vorliegenden schiefwinklig sphärischen Dreiecks in zwei rechtwinklig sphärische Dreiecke herbeigeführt werden.

Dazu wird von B das sphärische Lot auf AC bis D gefällt und es sei BD =v und 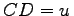 , also AD =b-u.
, also AD =b-u.
Aus den entsprechenden rechtwinkligen Dreiecken folgt:
 |
= |
 |
(3.218a) |
 |
= |
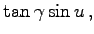 |
(3.218b) |
 |
= |
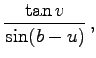 |
(3.218c) |
 |
= |
 |
(3.218d) |
Mit Hilfe von (3.218a) und (3.218d) kann der Winkel  berechnet werden.
berechnet werden.
![]()
![]() Geometrie Sphärische Trigonometrie Berechnung sphärischer Dreiecke Schiefwinklig sphärisches Dreieck
Geometrie Sphärische Trigonometrie Berechnung sphärischer Dreiecke Schiefwinklig sphärisches Dreieck
![]()
![]()
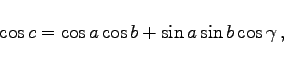
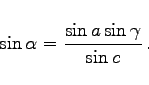
![]() kann im I. oder II. Quadranten liegen. Zwei Entscheidungsmöglichkeiten:
kann im I. oder II. Quadranten liegen. Zwei Entscheidungsmöglichkeiten: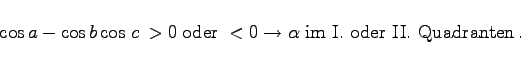
![]() bzw.
bzw. ![]() und
und ![]()
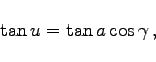


![]() und (oder)
und (oder) ![]()
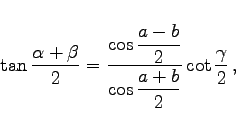

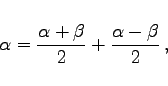

![]() Ausgangspunkt ist die Verwendung der Neperschen Gleichungen (3.204a) und (3.204b).
Ausgangspunkt ist die Verwendung der Neperschen Gleichungen (3.204a) und (3.204b).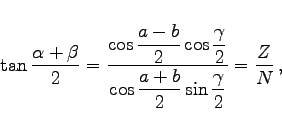
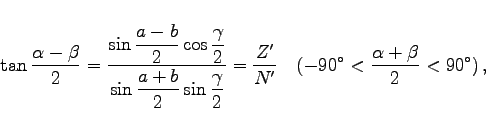

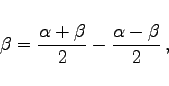


![]()
![]() , also AD =b-u.
, also AD =b-u.