Vektorielle Gleichungen

Die einfachsten vektoriellen Gleichungen sind in der folgenden Tabelle zusammengestellt. Darin sind die bekannten Vektoren; der gesuchte Vektor; die bekannten Skalare und x,y,z die gesuchten Skalare.

Tabelle Vektorielle Gleichungen

Gleichung	Lösung
1.
2.
3.	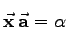Die Gleichung ist unbestimmt; trägt man alle Vektoren , die dieser Gleichung genügen, von einem Punkt aus ab, so liegen ihre Endpunkte auf einer Ebene, die auf dem Vektor senkrecht steht. Die Gleichung (3) nennt man die vektorielle Gleichung dieser Ebene.
4.	Die Gleichung ist unbestimmt; trägt man alle Vektoren , die dieser Gleichung genügen, von einem Punkt aus ab, so liegen ihre Endpunkte auf einer dem Vektor parallelen Geraden. Die Gleichung (4) nennt man die vektorielle Gleichung dieser Geraden.
5.
6.	wobei , , die zu , , reziproken Vektoren sind (vgl. reziproke Vektoren).
7.
8.