Lösungsverhalten

Aus der im Ergebnis der GAUSS-Schritte erhaltenen Matrix (4.116) liest man für das zu lösende inhomogene lineare Gleichungssystem ab:

1. Fall:

Das System ist unlösbar, wenn eine der Zahlen von Null verschieden ist.

2. Fall:

Das System ist lösbar, wenn gilt
Weiterhin ist zu unterscheiden:

1. r = n: Die Lösung ist eindeutig.
2. r < n: Die Lösung ist nicht eindeutig; n - r Unbekannte sind als Parameter frei wählbar.

Im Falle der Lösbarkeit werden die Unbekannten sukzessiv, mit der letzten Gleichung beginnend, aus dem gestaffelten Gleichungssystem, das zu (4.116) gehört, bestimmt.

Beispiel A

Nach drei GAUSS-Schritten hat die erweiterte Koeffizi- entenmatrix die Form

Die Lösung ist eindeutig, und aus dem zugehörigen gestaffelten linearen Gleichungssystem folgt .

Beispiel B

Nach zwei GAUSS-Schritten hat die erweiterte Koeffizientenmatrix die Form

Eine Lösung existiert, aber sie ist nicht eindeutig. Man kann eine Unbekannte als freien Parameter wählen, z.B. 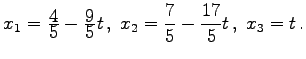und erhält: