Eigenschaften bezüglich des Eigenwertproblems

1. Anzahl der Eigenwerte:

Die Matrix hat genau n reelle Eigenwerte die entsprechend ihrer Vielfachheit zu zählen sind.

2. Orthogonalität der Eigenvektoren:

Die zu verschiedenen Eigenwerten gehörenden Eigenvektoren und sind orthogonal, d.h., es gilt

3. Matrix mit p-fachem Eigenwert:

Zu einem p-fachen Eigenwert existieren p linear unabhängige Eigenvektoren Wegen (4.124) sind auch alle nichttrivialen Linearkombinationen Eigenvektoren zu . Davon können p mit Hilfe des GRAM-SCHMIDTschen Orthogonalisierungsverfahrens ausgewählt werden, die orthogonal sind. Insgesamt gilt: Die Matrix besitzt genau n reelle orthogonale Eigenvektoren.

Beispiel

Die Eigenwerte sind und

Aus dem zugehörigen homogenen Gleichungssystem erhält man x₁ beliebig, x₂ beliebig, Man wählt und und erhält die beiden linear unabhängigen Eigenvektoren und wobei C₁ und C₂ beliebige Konstanten sind.

Man erhält x₁ beliebig, wählt z.B. x₁ = 1 und erhält den Eigenvektor wobei C₃ eine beliebige Konstante ist. Die Matrix ist symmetrisch, die zu den verschiedenen Eigenwerten gehörenden Eigenvektoren sind orthogonal.

Gram-Schmidtsches Orthogonalisierungsverfahren

Es sei V_n ein beliebiger n-dimensionaler EUKLIDischer Vektorraum. Die Vektoren seien linear unabhängig. Dann existiert ein Orthogonalsystem von Vektoren , das auf folgende Weise konstruiert werden kann:

Hinweise:
1. Mit wird das Skalarprodukt der Vektoren und bezeichnet.
2. Zu dem Orthogonalsystem der Vektoren erhält man das Orthonormalsystem durch 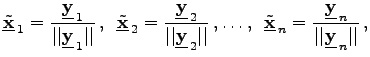wobei mit 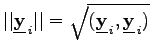die EUKLIDische Norm des Vektors bezeichnet wird.

Beispiel

. Daraus folgt:
und ;  und ;
und .