Inhalt Index DeskTop Bronstein
![]()
![]() Lineare Algebra Eigenwertaufgaben bei Matrizen Singulärwertzerlegung
Lineare Algebra Eigenwertaufgaben bei Matrizen Singulärwertzerlegung
Wenn ![]() eine reelle Matrix vom Typ (m,n) mit dem Rang r ist, dann heißen die positiven Wurzeln
eine reelle Matrix vom Typ (m,n) mit dem Rang r ist, dann heißen die positiven Wurzeln ![]() aus den Eigenwerten
aus den Eigenwerten ![]() der Matrix
der Matrix ![]() Singulärwerte der Matrix A. Die zugehörigen Eigenvektoren
Singulärwerte der Matrix A. Die zugehörigen Eigenvektoren ![]() von
von ![]() heißen Rechtssingulärvektoren von A, die zugehörigen Eigenvektoren
heißen Rechtssingulärvektoren von A, die zugehörigen Eigenvektoren ![]() von
von ![]() Linkssingulärvektoren. Dabei besitzt die Matrix
Linkssingulärvektoren. Dabei besitzt die Matrix ![]() dieselben r von Null verschiedenen Eigenwerte
dieselben r von Null verschiedenen Eigenwerte ![]() wie die Matrix
wie die Matrix ![]()
 |
(4.152a) |
Außerdem besteht zwischen den Rechts- und Linkssingulärvektoren der Zusammenhang
 |
(4.152b) |
Es gilt: Eine Matrix ![]() vom Typ (m,n) mit dem Rang r besitzt r positive Singulärwerte
vom Typ (m,n) mit dem Rang r besitzt r positive Singulärwerte ![]() Dazu existieren r orthonormierte Rechtssingulärvektoren
Dazu existieren r orthonormierte Rechtssingulärvektoren ![]() und r orthonormierte Linkssingulärvektoren
und r orthonormierte Linkssingulärvektoren ![]() Darüber hinaus existieren zum Singulärwert Null n - r orthonormierte Rechtssingulärvektoren
Darüber hinaus existieren zum Singulärwert Null n - r orthonormierte Rechtssingulärvektoren ![]() und m-r orthonormierte Linkssingulärvektoren
und m-r orthonormierte Linkssingulärvektoren ![]() Eine Matrix vom Typ (m,n) hat demzufolge n Rechtssingulärvektoren und m Linkssingulärvektoren, die man zu den orthogonalen Matrizen
Eine Matrix vom Typ (m,n) hat demzufolge n Rechtssingulärvektoren und m Linkssingulärvektoren, die man zu den orthogonalen Matrizen
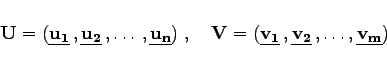 |
(4.153) |
zusammenfassen kann.