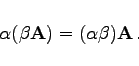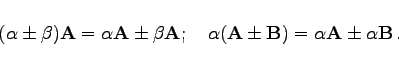Multiplikation einer Matrix mit einer Zahl
Eine Matrix  vom Typ (m,n) wird mit einer reellen oder komplexen Zahl
vom Typ (m,n) wird mit einer reellen oder komplexen Zahl 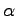 multipliziert, indem jedes Element von
multipliziert, indem jedes Element von  mit
mit 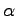 multipliziert wird:
multipliziert wird:
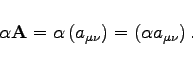 |
(4.22a) |
| Beispiel |
|
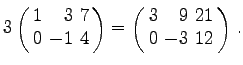
|
Mit (4.22a) wird auch ausgesagt, daß ein konstanter Faktor, der in allen Elementen einer Matrix enthalten ist, ausgeklammert werden kann.
Die Division einer Matrix durch einen Skalar wird als Multiplikation mit  durchgeführt, wobei
durchgeführt, wobei  sein muß.
sein muß.
Es gelten das Kommutativ-, Assoziativ- und Distributivgesetz der Multiplikation einer Matrix mit einem Skalar:
- Kommutativgesetz:
-
 |
(4.22b) |
- Assoziativgesetz:
-
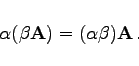 |
(4.22c) |
- Distributivgesetz:
-
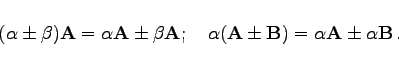 |
(4.22d) |
![]() vom Typ (m,n) wird mit einer reellen oder komplexen Zahl
vom Typ (m,n) wird mit einer reellen oder komplexen Zahl ![]() multipliziert, indem jedes Element von
multipliziert, indem jedes Element von ![]() mit
mit ![]() multipliziert wird:
multipliziert wird:![]() durchgeführt, wobei
durchgeführt, wobei ![]() sein muß.
sein muß.