Inhalt Index DeskTop Bronstein
![]()
![]() Algebra und Diskrete Mathematik Klassische algebraische Strukturen Vektorräume
Algebra und Diskrete Mathematik Klassische algebraische Strukturen Vektorräume
Ein Vektorraum über einem Körper K (K-Vektorraum) besteht aus einer additiv geschriebenen ABELschen Gruppe V=(V,+) von Vektoren , einem Körper ![]() von Skalaren und einer äußeren Multiplikation
von Skalaren und einer äußeren Multiplikation ![]() die jedem geordneten Paar (k,v) mit
die jedem geordneten Paar (k,v) mit ![]() und
und ![]() einen Vektor
einen Vektor ![]() zuordnet. Dabei gelten folgende Gesetze:
zuordnet. Dabei gelten folgende Gesetze:
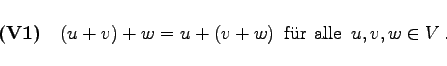 |
(5.210) |
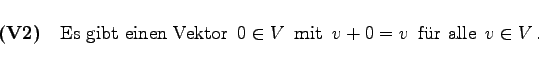 |
(5.211) |
 |
(5.212) |
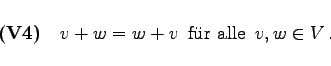 |
(5.213) |
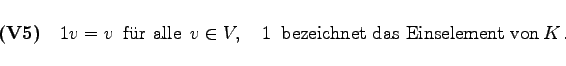 |
(5.214) |
 |
(5.215) |
 |
(5.216) |
 |
(5.217) |
Ist ![]() , so spricht man von einem reellen Vektorraum .
, so spricht man von einem reellen Vektorraum .
| Beispiel A |
|
Einspaltige bzw. einzeilige reelle Matrizen vom Typ (n,1) bzw. (1,n) bilden bezüglich der Matrizenaddition und der äußeren Multiplikation mit einer reellen Zahl einen reellen Vektorraum |
| Beispiel B |
|
Alle reellen Matrizen vom Typ (m,n) bilden einen reellen Vektorraum. |
| Beispiel C | ||
|
Alle auf einem Intervall [a,b] stetigen reellen Funktionen bilden mit den durch
definierten Operationen einen reellen Vektorraum. Funktionenräume spielen in der Funktionalanalysis eine wesentliche Rolle. |