Inhalt Index DeskTop Bronstein
![]()
![]() Algebra und Diskrete Mathematik Elementare Zahlentheorie Sätze von Fermat, Euler und Wilson
Algebra und Diskrete Mathematik Elementare Zahlentheorie Sätze von Fermat, Euler und Wilson
Für jede natürliche Zahl m mit m > 0 kann man die Anzahl der zu m teilerfremden Zahlen x mit ![]() angeben. Die zugehörige Funkion
angeben. Die zugehörige Funkion ![]() wird EULERsche Funktion genannt. Der Funktionswert
wird EULERsche Funktion genannt. Der Funktionswert ![]() ist die Anzahl der primen Restklassen modulo m (s. Prime Restklassen).
ist die Anzahl der primen Restklassen modulo m (s. Prime Restklassen).
Es gilt ![]() usw. Allgemein gilt
usw. Allgemein gilt ![]() für jede Primzahl p und
für jede Primzahl p und ![]() für jede Primzahlpotenz
für jede Primzahlpotenz ![]() Ist m eine beliebige natürliche Zahl, dann kann man
Ist m eine beliebige natürliche Zahl, dann kann man ![]() wie folgt berechnen:
wie folgt berechnen:
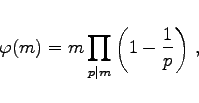 |
(5.283a) |
wobei das Produkt über alle Primteiler p von m zu erstrecken ist.
| Beispiel |
|
|
Außerdem gilt
 |
(5.283b) |
Gilt ![]() , dann ist
, dann ist ![]()
| Beispiel |
|
|