Inhalt Index DeskTop Bronstein
![]()
![]() Algebra und Diskrete Mathematik Fuzzy-Logik Verknüpfungen unscharfer Mengen Praktische Verknüpfungen unscharfer Mengen
Algebra und Diskrete Mathematik Fuzzy-Logik Verknüpfungen unscharfer Mengen Praktische Verknüpfungen unscharfer Mengen
wobei gilt:
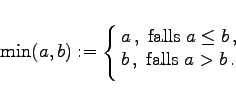 |
(5.375b) |
Der Schnittoperation entspricht die UND-Operation zweier Zugehörigkeitsfunktionen (s. linke Abbildung). Die Zugehörigkeitsfunktion ![]() definiert den minimalen Wert, gebildet aus
definiert den minimalen Wert, gebildet aus ![]() und
und ![]()
wobei gilt:
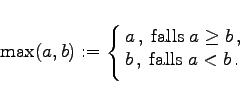 |
(5.376b) |
Die Vereinigung enstpricht der logischen ODER-Verknüpfung (rechte Abbildung). Die Darstellung zeigt ![]() als den maximalen Wert der jeweiligen Zugehörigkeitsfunktionen
als den maximalen Wert der jeweiligen Zugehörigkeitsfunktionen ![]() und
und ![]() .
.
| Beispiel |
|
Die t-Norm |
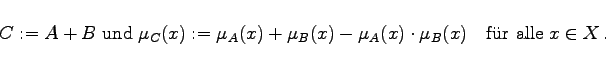 |
(5.377a) |
Wie die Vereinigung (5.376a,b) gehören die genannten Summen zu den s-Normen. Sie sind in vereinfachter Schreibweise in der rechten Spalte der Tabelle der t- und s-Normen zu finden.
In Analogie zum erweiterten Summenbegriff für die Vereinigungsbildung ergeben sich für die Durchschnittsbildung mit Hilfe des beschränkten, des algebraischen und des drastischen Produktes entsprechende Erweiterungen. So ist z.B. das algebraische Produkt wie folgt definiert:
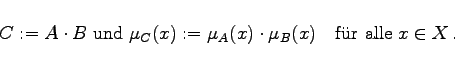 |
(5.377b) |
Es gehört wie die Durchschnittsbildung (5.375a,b) zu den t-Normen, die in der mittleren Spalte von Tabelle der t- und s-Normen zu finden sind.