Inhalt Index DeskTop Bronstein
![]()
![]() Differentialrechnung Differentiation von Funktionen einer Veränderlichen Differentiationsregeln für Funktionen einer Veränderlichen Grundregeln für das Differenzieren
Differentialrechnung Differentiation von Funktionen einer Veränderlichen Differentiationsregeln für Funktionen einer Veränderlichen Grundregeln für das Differenzieren
Im Falle von y(x)>0 kann man zur Berechnung der Ableitung y' von der Funktion ![]() ausgehen, für deren Ableitung (unter Berücksichtigung der Kettenregel) gilt:
ausgehen, für deren Ableitung (unter Berücksichtigung der Kettenregel) gilt:
 |
(6.11) |
Daraus folgt unmittelbar
Mit Hilfe der logarithmischen Differentiation lassen sich viele Differentiationsaufgaben wesentlich vereinfachen bzw. überhaupt erst durchführen. Letzteres trifft z.B. auf Funktionen der Form
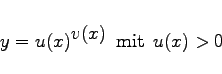 |
(6.13) |
zu. Die logarithmische Differentiation dieser Gleichung ergibt gemäß (6.12)
 |
(6.14) |
| Beispiel |
|
|
Die logarithmische Differentiation wird häufig angewendet, wenn ein Produkt von Funktionen zu differenzieren ist.
| Beispiel A |
|
|
| Beispiel B |
|
|
| Beispiel C |
|
|