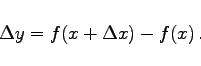Begriff des Differentials
Für jede der Variablen 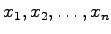 läßt sich ein Differential
läßt sich ein Differential 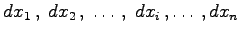 bilden. Die Definition fällt unterschiedlich aus, je nachdem, ob es sich um das Differential einer unabhängigen Variablen oder um das einer Funktion handelt:
bilden. Die Definition fällt unterschiedlich aus, je nachdem, ob es sich um das Differential einer unabhängigen Variablen oder um das einer Funktion handelt:
- 1. Differential einer unabhängigen Variablen x
- nennt man den Zuwachs der Größe x gemäß
 |
(6.37a) |
Dabei kann man 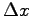 einen beliebigen Wert beimessen.
einen beliebigen Wert beimessen.
- 2. Differential einer Funktion y = f(x) einer Veränderlichen x
- nennt man für einen gegebenen x-Wert und einen gegebenen Wert des Differentials dx das Produkt
 |
(6.37b) |
- 3. Zuwachs (Inkrement)
 einer Funktion y=f(x) von x nach
einer Funktion y=f(x) von x nach  nennt man die Differenz
nennt man die Differenz
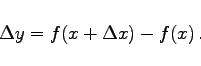 |
(6.37c) |
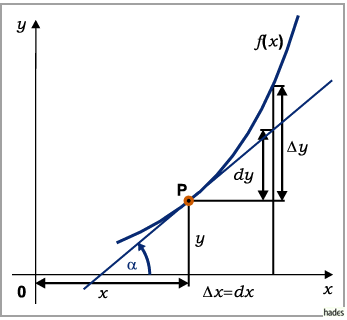
- 4. Geometrische Bedeutung des Differentials:
- Wenn die Funktion durch eine Kurve in einem kartesischen Koordinatensystem dargestellt ist, dann ist dy der Zuwachs, den die Ordinate der Kurventangente im Punkt x für einen gegebenen Zuwachs dx erfährt.
![]()
![]() Differentialrechnung Differentiation von Funktionen von mehreren Veränderlichen Partielle Ableitungen
Differentialrechnung Differentiation von Funktionen von mehreren Veränderlichen Partielle Ableitungen
![]() läßt sich ein Differential
läßt sich ein Differential ![]() bilden. Die Definition fällt unterschiedlich aus, je nachdem, ob es sich um das Differential einer unabhängigen Variablen oder um das einer Funktion handelt:
bilden. Die Definition fällt unterschiedlich aus, je nachdem, ob es sich um das Differential einer unabhängigen Variablen oder um das einer Funktion handelt:
![]() einen beliebigen Wert beimessen.
einen beliebigen Wert beimessen.