Inhalt Index DeskTop Bronstein
![]()
![]() Unendliche Reihen Reihen mit konstanten Gliedern Konvergenzkriterien für Reihen mit positiven Gliedern
Unendliche Reihen Reihen mit konstanten Gliedern Konvergenzkriterien für Reihen mit positiven Gliedern
Wenn für die Reihe
 |
(7.25a) |
von einem gewissen n an alle Quotienten ![]() kleiner sind als eine Zahl
kleiner sind als eine Zahl ![]() , dann ist die Reihe konvergent:
, dann ist die Reihe konvergent:
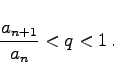 |
(7.25b) |
Wenn diese Quotienten von einem gewissen n an größer sind als eine Zahl ![]() , dann ist die Reihe divergent. Daraus ergibt sich: Gilt
, dann ist die Reihe divergent. Daraus ergibt sich: Gilt
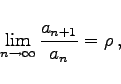 |
(7.25c) |
dann ist die Reihe für ![]() konvergent und für
konvergent und für ![]() divergent. Für
divergent. Für ![]() kann mit dem Quotientenkriterium keine Aussage über das Konvergenzverhalten gemacht werden.
kann mit dem Quotientenkriterium keine Aussage über das Konvergenzverhalten gemacht werden.
| Beispiel A |
|
Die Reihe |
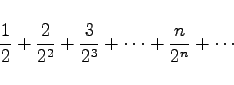 |
(7.26a) |
konvergiert, denn es gilt
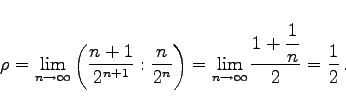 |
(7.26b) |
| Beispiel B |
|
Für die Reihe |
liefert das Quotientenkriterium wegen
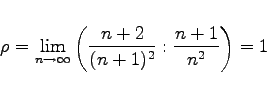 |
(7.27b) |
keine Entscheidung über die Konvergenz oder Divergenz der Reihe.