Inhalt Index DeskTop Bronstein
![]()
![]() Unendliche Reihen Reihen mit konstanten Gliedern Konvergenzkriterien für Reihen mit positiven Gliedern
Unendliche Reihen Reihen mit konstanten Gliedern Konvergenzkriterien für Reihen mit positiven Gliedern
Gilt für eine Reihe
 |
(7.28a) |
von einem gewissen n an für alle Zahlen ![]()
 |
(7.28b) |
dann ist die Reihe konvergent. Sind umgekehrt von einem gewissen n an alle Zahlen ![]() größer als eine Zahl Q und ist
größer als eine Zahl Q und ist ![]() , dann divergiert die Reihe. Daraus ergibt sich: Gilt
, dann divergiert die Reihe. Daraus ergibt sich: Gilt
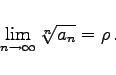 |
(7.28c) |
dann ist die Reihe konvergent für ![]() und divergent für
und divergent für ![]() . Für
. Für ![]() kann mit dem Wurzelkriterium keine Aussage über das Konvergenzverhalten gemacht werden.
kann mit dem Wurzelkriterium keine Aussage über das Konvergenzverhalten gemacht werden.
| Beispiel |
|
Die Reihe |
 |
(7.29a) |
ist konvergent wegen
 |
(7.29b) |