Asymptotische Potenzreihen

1. Begriff der asymptotischen Potenzreihe:

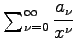Eine Reihe heißt asymptotische Potenzreihe der Funktion , die für x > x₀ definiert ist, wenn

für jedes gilt. Dabei wird in das LANDAU-Symbol groß O  verwendet. Für (7.92) schreibt man auch .

2. Eigenschaften asymptotischer Potenzreihen:

a) Eindeutigkeit:

Existiert für eine Funktion f(x) die asymptotische Potenzreihe, dann ist sie eindeutig, aber durch eine asymptotische Potenzreihe ist eine Funktion nicht eindeutig bestimmt.

b) Konvergenz:

Von einer asymptotischen Potenzreihe muß keine Konvergenz gefordert werden.

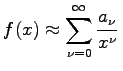Beispiel A

ist eine asymptotische Reihe, die für alle x mit konvergiert.

Beispiel B

Wiederholte partielle Integration ergibt für das Parameterintegral , das für x > 0 konvergiert, die Darstellung mit . Wegen gilt und damit

Die asymptotische Potenzreihe (7.93) ist divergent für alle , da der Betrag des Quotienten aus dem (n+1)-ten und dem n-ten Glied den Wert hat. Trotzdem ist diese divergente Reihe zur Funktionswertberechnung von f(x) gut geeignet. So erhält man z.B. für x=10 mit Hilfe der Partialsummen S₄(10) und S₅(10) die Abschätzung 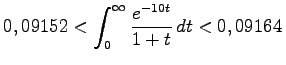.