Dirichletsche Bedingungen

Wenn die Funktion f(x) die DIRICHLETschen Bedingungen erfüllt, d.h. wenn

1. das Definitionsintervall in endlich viele Intervalle zerlegt werden kann, in denen die Funktion f(x) stetig und monoton ist, und
2. an jeder Unstetigkeitsstelle von f(x) die Werte f(x+0) und f(x-0) definiert sind,

dann konvergiert die FOURIER-Reihe dieser Funktion. Der Summenwert der Reihe ist dort, wo f(x) stetig ist, gleich , in den Unstetigkeitsstellen gleich 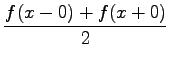.