Inhalt Index DeskTop Bronstein
![]()
![]() Unendliche Reihen Fourier-Reihen Koeffizientenbestimmung für symmetrische Funktionen
Unendliche Reihen Fourier-Reihen Koeffizientenbestimmung für symmetrische Funktionen
Jede Funktion ![]() , die in einem Intervall
, die in einem Intervall ![]() die DIRICHLETschen Bedingungen erfüllt, kann in diesem Intervall in konvergente Reihen folgender Formen entwickelt werden:
die DIRICHLETschen Bedingungen erfüllt, kann in diesem Intervall in konvergente Reihen folgender Formen entwickelt werden:
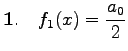 |
+ | 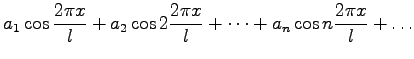 |
|
| + | 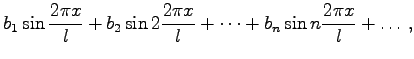 |
(7.105a) |
In den Unstetigkeitsstellen wird 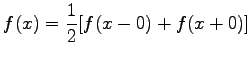 gesetzt. Die Entwicklungskoeffizienten werden mit Hilfe der EULERschen Formeln (7.95a,b) für
gesetzt. Die Entwicklungskoeffizienten werden mit Hilfe der EULERschen Formeln (7.95a,b) für 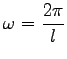 bestimmt.
bestimmt.
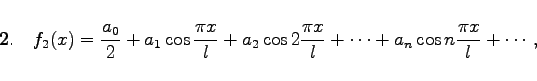 |
(7.105b) |
Die Periode der Funktion f2(x) ist T = 2l; im Intervall ![]() ist f2(x) von der Symmetrie 1. Art und identisch mit
ist f2(x) von der Symmetrie 1. Art und identisch mit ![]() .
.
Die Entwicklungskoeffizienten für f2(x) werden nach den Formeln für den Fall der Symmetrie 1. Art mit T = 2l bestimmt.
 |
(7.105c) |
Die Periode der Funktion f3(x) ist ![]() , im Intervall 0 < x < l ist f3(x) von der Symmetrie 2. Art und identisch mit
, im Intervall 0 < x < l ist f3(x) von der Symmetrie 2. Art und identisch mit ![]() .
.
Die Entwicklungskoeffizienten werden mit den Formeln für den Fall der Symmetrie 2. Art (7.101) für T = 2l bestimmt.