Fourier-Darstellung periodischer Funktionen (Fourier-Analyse)
Oft ist es notwendig oder vorteilhaft, eine gegebene periodische Funktion f(x) mit der Periode T exakt oder angenähert durch eine Summe aus trigonometrischen Funktionen in der Form
| sn (x) |
= |
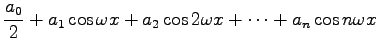 |
|
| |
|
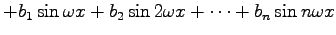 |
(7.94) |
darzustellen. Man spricht von FOURIER-Entwicklung. Dabei gilt für die Kreisfrequenz  . Im Falle
. Im Falle  ist
ist  . Die beste Approximation von f(x) in dem unter Wichtigste Eigenschaften von FOURIER-Reihen angegebenen Sinne erreicht man mit einer Näherungsfunktion
. Die beste Approximation von f(x) in dem unter Wichtigste Eigenschaften von FOURIER-Reihen angegebenen Sinne erreicht man mit einer Näherungsfunktion  , wenn für die Koeffizienten ak und bk mit
, wenn für die Koeffizienten ak und bk mit  die FOURIER-Koeffizienten der gegebenen Funktion gewählt werden. Ihre Bestimmung geschieht analytisch mit Hilfe der EULERschen Formeln
die FOURIER-Koeffizienten der gegebenen Funktion gewählt werden. Ihre Bestimmung geschieht analytisch mit Hilfe der EULERschen Formeln
| ak |
= |
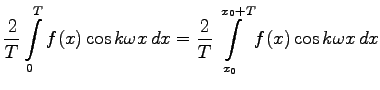 |
|
| |
= |
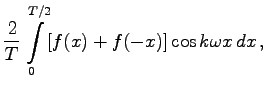 |
(7.95a) |
und
| bk |
= |
 |
|
| |
= |
 |
(7.95b) |
oder näherungsweise mit Hilfe der harmonischen Analyse.
![]()
![]() Unendliche Reihen Fourier-Reihen Trigonometrische Summe und Fourier-Reihe Grundbegriffe
Unendliche Reihen Fourier-Reihen Trigonometrische Summe und Fourier-Reihe Grundbegriffe
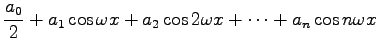
 . Im Falle
. Im Falle 
