Inhalt Index DeskTop Bronstein
![]()
![]() Integralrechnung Mehrfachintegrale Doppelintegral Berechnung des Doppelintegrals
Integralrechnung Mehrfachintegrale Doppelintegral Berechnung des Doppelintegrals
Die Koordinaten sind in Parameterform durch die Beziehungen
 |
(8.138) |
definiert. Das Flächenstück wird durch die Koordinatenlinien u = const und v = const in infinitesimale Flächenelemente eingeteilt (s. Abbildung) und der Integrand in den Koordinaten u und v ausgedrückt.
Summiert wird zuerst längs eines Koordinatenstreifens, z.B. längs v = const, danach über alle Streifen:
Dabei sind v = v1(u) bzw. v = v2(u) die Gleichungen der inneren bzw. äußeren Randkurve ![]() und
und ![]() der Fläche
der Fläche ![]() . Mit u1 und u2 werden die Koordinaten der beiden äußersten Linienbegrenzungen der Fläche S beschrieben. Mit |D| ist der Absolutbetrag der Funktionaldeterminante
. Mit u1 und u2 werden die Koordinaten der beiden äußersten Linienbegrenzungen der Fläche S beschrieben. Mit |D| ist der Absolutbetrag der Funktionaldeterminante
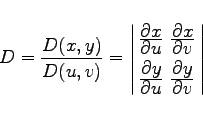 |
(8.140a) |
bezeichnet, mit deren Hilfe das Flächenelement in krummlinigen Koordinaten beschrieben wird:
 |
(8.140b) |
Die Formel (8.137b) ist ein Spezialfall von Formel (8.139) für die Polarkoordinaten ![]() . Die Funktionaldeterminate ergibt sich hier zu
. Die Funktionaldeterminate ergibt sich hier zu ![]() .
.
Man wählt die krummlinigen Koordinaten derart, daß die Integrationsgrenzen des Integrals (8.139) möglichst einfach werden.
| Beispiel |
|
|
Zuerst werden die krummlinigen Koordinaten ![]() eingeführt, deren Koordinatenlinien u = c1 eine Schar ähnlicher Astroiden mit den Gleichungen
eingeführt, deren Koordinatenlinien u = c1 eine Schar ähnlicher Astroiden mit den Gleichungen ![]() und
und ![]() darstellen. Die Koordinatenlinien v = c2 sind dann Strahlen mit der Gleichung
darstellen. Die Koordinatenlinien v = c2 sind dann Strahlen mit der Gleichung ![]() , wobei
, wobei ![]() gilt. Damit ergibt sich
gilt. Damit ergibt sich
 ,
,
 .
.