Inhalt Index DeskTop Bronstein
![]()
![]() Integralrechnung Oberflächenintegrale Oberflächenintegrale 1. Art Berechnung des Oberflächenintegrals 1. Art
Integralrechnung Oberflächenintegrale Oberflächenintegrale 1. Art Berechnung des Oberflächenintegrals 1. Art
Ist die Fläche S durch die Gleichung
wobei S' die Projektion von S auf die x,y-Ebene ist und p und q die partiellen Ableitungen 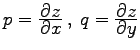 sind. Dabei wird vorausgesetzt, daß jedem Punkt der Fläche S in der x,y-Ebene eindeutig ein Punkt ihrer Projektion S' entspricht, d.h., der Flächenpunkt muß eindeutig durch seine Koordinaten definiert sein. Sollte das nicht der Fall sein, dann wird das Flächenstück S in einige Teilflächenstücke eingeteilt, so daß das Integral über die gesamte Fläche als algebraische Summe der Integrale über die Teilflächenstücke von S dargestellt werden kann. Ist die Fläche in Parameterform gegeben, dann entfällt diese Einschränkung.
sind. Dabei wird vorausgesetzt, daß jedem Punkt der Fläche S in der x,y-Ebene eindeutig ein Punkt ihrer Projektion S' entspricht, d.h., der Flächenpunkt muß eindeutig durch seine Koordinaten definiert sein. Sollte das nicht der Fall sein, dann wird das Flächenstück S in einige Teilflächenstücke eingeteilt, so daß das Integral über die gesamte Fläche als algebraische Summe der Integrale über die Teilflächenstücke von S dargestellt werden kann. Ist die Fläche in Parameterform gegeben, dann entfällt diese Einschränkung.
Die Gleichung (8.151a) kann auch in der anderen Form
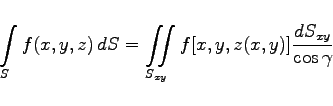 |
(8.151b) |
dargestellt werden. Das hängt damit zusammen, daß die Gleichung der Flächennormalen von (8.150) die Form 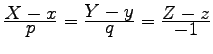 hat, so daß für den Winkel zwischen der Normalenrichtung und der z-Achse die Beziehung
hat, so daß für den Winkel zwischen der Normalenrichtung und der z-Achse die Beziehung ![]() besteht. Bei der Berechnung eines Oberflächenintegrals 1. Art faßt man diesen Winkel
besteht. Bei der Berechnung eines Oberflächenintegrals 1. Art faßt man diesen Winkel ![]() als spitzen Winkel auf, so daß immer
als spitzen Winkel auf, so daß immer ![]() ist.
ist.