Inhalt Index DeskTop Bronstein
![]()
![]() Differentialgleichungen Gewöhnliche Differentialgleichungen Randwertprobleme Entwicklung nach Eigenfunktionen
Differentialgleichungen Gewöhnliche Differentialgleichungen Randwertprobleme Entwicklung nach Eigenfunktionen
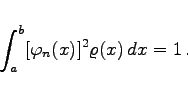 |
(9.75a) |
Man spricht dann von einer normierten Eigenfunktion.
nach den Eigenfunktionen des zugehörigen Randwertproblems zugeordnet werden, sofern die Integrale in (9.75b) sinnvoll sind.
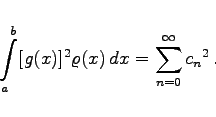 |
(9.75c) |
Die FOURIER-Reihe der Funktion g(x) konvergiert in diesem Falle im Mittel gegen ![]() , d.h., es gilt
, d.h., es gilt
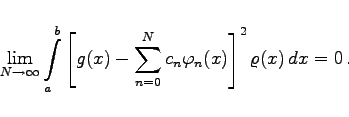 |
(9.75d) |